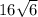куб. ед.
Пошаговое объяснение:
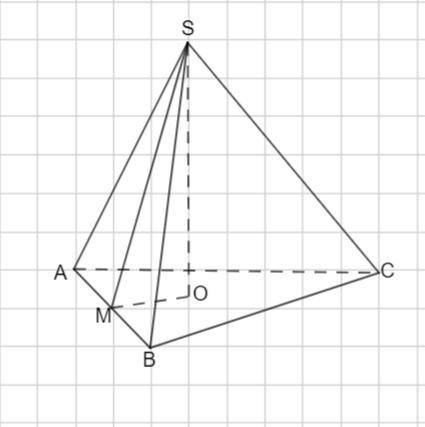
Пусть SABC -правильная треугольная пирамида.
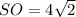ед.
S(бок)=3S(осн)
Так как пирамида правильная, то треугольник АВС - правильный. Пусть сторона треугольника будет а.
Тогда площадь основания буден равна
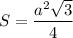
S(бок)=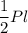 
, где Р- периметр основания, а 
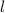- апофема.
Так как площадь боковой поверхности в 3 раза больше площади основания, то
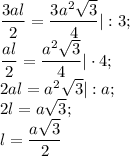
Рассмотрим треугольник SOM - прямоугольный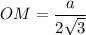 
, как радиус окружности , вписанной в правильный треугольник АВС.
Применим теорему Пифагора: в прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Объем пирамиду определяется по формуле:
где 
площадь основания, а Н - высота пирамиды.
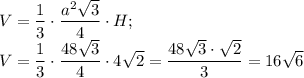
Значит, объем пирамиды равен 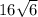куб. ед.
6) приравниваем выражение под модулем к нулю. x=3/4
Нарисуем интервал и разобьём его на 2 отрезка: (-беск. до 3/4] и (3/4 до +беск.)
Берём из первого интервала любое число, например -100. Подставляем в выражение 4x-3. Получается отрицательное число, значит знак на интервале (-беск. до 3/4] "-".
Аналогично, для второго интервала, берём число 100, подставляем. Знак интервала (3/4 до +беск.) "+".
Раскрываем модуль на 1-ом интервале:
-7/3(4x-3)+7,2=9
x= 39/70
Проверяем на интервале (-беск. до 3/4]
Данное число входит в этот интервал, значит является корнем.
Также на 2-ом, со знаком "+".
7/3(4x-3)+7,2=9
x=33/35
Проверяем на интервале (3/4 до +беск.). Данный корень является решением
ответ: x=39/70, x2=33/35
