ответ: 15 см.
Дано: Параллелепипед - аквариум.
a = 60 см длина
b = 50 см ширина
c = 40 см - высота
v = 75 л - объём воды.
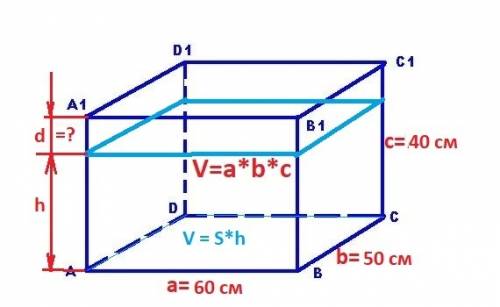
Найти: d = ? - расстояние до верха аквариума.
Пошаговое объяснение:
Рисунок к задаче в приложении.
1 л = 1000 см³ - единицы объёма.
Объём аквариума по формуле:
V = a*b*c = 60*50*40 = 120 000 см³ = 120 л - аквариум.
Можно составить пропорцию для высоты воды.
40 см : 120 л = h : 75 л
h = 40 * 75/120 = 25 см - высота воды.
d = c - h = 40 - 25 = 15 см - до края аквариума - ответ.
Или по другой формуле:
v = 75 л = 75 000 см³ - объём воды.
v = S*h = a*b*h = 60*50*h = 300*h = 75 000
h = 75000 : 300 = 25 см - уровень воды.
d = c - h = 40 - 25 = 15 см - ответ.
Вот решение
Пошаговое объяснение:
Решение.
Введем систему координат так, как показано на рисунке:
O – начало координат.
Оси направлены по диагоналям квадрата основания и по высоте пирамиды.
1) SABCD – правильная пирамида □(⇒┴ ) ABCD – квадрат, AC BD,
AD2 = AO2 + AO2,
2AO2 = 4, AO2 = 2,
AO = √2, AO = OD = √2.
Угол между прямой AC и плоскостью ASD, значит, определим координаты следующих точек:
A(√2;0;0) , C(-√2;0;0) □(⇒┴ ) (AC) ⃗{-2√2;0;0}.
2) Для уравнения плоскости ASD найдём SO:
SO (ABC) □(⇒┴ ) SO AO = SO2 = AS2 – AO2,
SO = √(25-2)=√23 □(⇒┴ )
S(0;0; √23 ), A(√2;0;0) , D(0; √2;0).
полагая d = -√2 , получим: a = 1, b = 1, c = √2/√23=√46/23 .
Получим уравнение плоскости: x + y +√46/23 z - √2 = 0, □(⇒┴ ) n ⃗ {1;1;√46/23} .
|((AC) ⃗*n ⃗ ) |=|-2√2+0+0|=2√(2.)
|(AC) ⃗ |=√8=2√(2;)
|n ⃗ |=√(1+1+46/23)=√(2+2/23)=√(48/23)
sinα=√69/12,α=arcsin √69/12.
ответ: α=arcsin √69/12 .
120*0,55=66(учеников) - пятиклассников
ответ 66 пятиклассников