В правильной пирамиде медиана боковой грани к основанию - это апофема А.
Сторона основания а и основание боковой грани а равны по 1.
Находим апофему: A = 2S/a = 2*1/1 = 2.
По свойству медиан точка М делит апофему в отношении 2:1 от вершины. SM = (2/3)*2 = 4/3, МК = (1/3)*2 = 2/3.
Находим высоту пирамиды: H = √(2² - (1/2)²) = √15/2.
Находим косинус и синус угла α между основанием пирамиды и боковой гранью.
cos α = (1/2)/2 = 1/4, sin α = (√15/2)/2 = √15/4.
Косинус угла при вершине пирамиды (назовём его S) равен:
cos S = (22 + 22 – 12)/(2*2*2) = 7/8, синус равен √(1 – (49/64)) = √15/8.
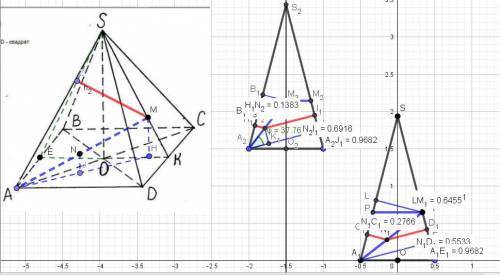
Проведём два осевых сечения пирамиды перпендикулярно смежным сторонам основания и спроецируем на эти плоскости точки M и N (они даны на прилагаемых рисунках).
Расстояния от точек М и N до граней пирамиды обозначим буквой h.
До основания: h(М) = (1/3) H = (1/3)*(√15/2) = √15/6.
h(N) = (3/7) hM = (3/7)*(√15/6) = √15/14.
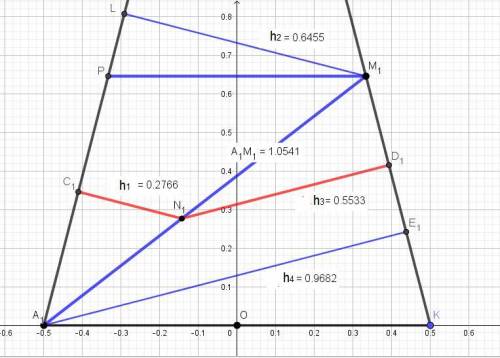
До грани, содержащую точку М, и противоположную ей.
Высота h2 = SM*sin S = (4/3)*(√15/8) = √15/6.
h1 = (3/7) h2 = (3/7)*(√15/6) = √15/14.
Высота h4 = a*sin α = 1*(√15/4) = √15/4.
h3 = (4/7) h4 = (4/7)*(√15/4) = √15/7.
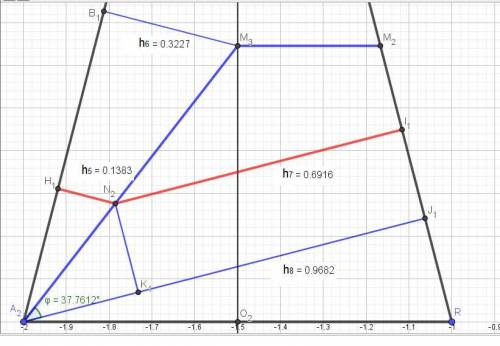
Рассмотрим второе сечение.
Высота h6 = SM3*sin (S/2) = (2/3)*H*((1/2)/2) = (2/3)*(√15/2)*(1/4) = √15/12.
h5 = (3/7) h6 = (3/7)*(√15/12) = √15/28.
Высота h8 = a*sin α = 1*(√15/4) = √15/4.
Для определения высоты h7 найдём угол φ.
φ = arc tg(M3O/(a/2)) – (90º - arc sin α) = arc tg((√15/6)/(1/2)) – arc sin(√15/4) = arc tg((√15/3) – arc sin(√15/4) = 52,23875609º – (90º - 75,52248781º) =
= 37,76124391º.
cos φ = 0,790569.
Найдём длину проекции отрезка АМ на секущую плоскость SEK по теореме косинусов: AM = √(12 + (2/3)² - 2*1*(2/3)*(1/4)) = √(1 + (4/9) – (1/3)) = √10/3.
Тогда AN = (3/7)AM = (3/7)*( √10/3) = √10/7.
Отсюда h7 = h8 – AN*cos φ = √15/4 – (√15/7)*0,790569 = 0,691604.
Сложим длины всех заданных высот:
Σh = (√15/14) + (√15/14) + (√15/7) + (√15/28) + 0,691604 = 1,936492.
 часть всех запасов сахара для дрессуры, то у него осталась
часть всех запасов сахара для дрессуры, то у него осталась 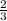 запасов сахара для дрессуры, т.е. в
запасов сахара для дрессуры, т.е. в  раза больше, чем он потратил. Поскольку
раза больше, чем он потратил. Поскольку 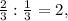 или иначе говоря, поскольку
или иначе говоря, поскольку 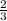 вдвое больше, чем
вдвое больше, чем 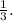
 кусков сахара.
кусков сахара. недели.
недели. недель.
недель.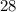 кусков сахара за
кусков сахара за  недели, а значит, в неделю он тратил в два раза меньше, т.е.
недели, а значит, в неделю он тратил в два раза меньше, т.е. 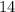 кусков сахара в неделю.
кусков сахара в неделю. кусков сахара в неделю.
кусков сахара в неделю.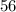 кусков после начальной дрессуры, то при расходе
кусков после начальной дрессуры, то при расходе  кусков сахара в неделю ему хватит этого остаточного запаса на
кусков сахара в неделю ему хватит этого остаточного запаса на 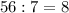 недель.
недель. недель.
недель.
х+1,8 - скорость по течению
х-1,8 - скорость против течения
5(х-1,8)=4(х+1,8)
5х-9=4х+7,2
5х-4х=7,2+9
х=16,2 (км/ч)
ответ: скорость катера в стоячей воде 16,2 км/ч