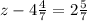
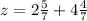
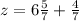
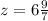
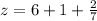
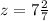
Пошаговое объяснение:
Число кратно 5, то есть оно должно кончаться на 0 или на 5.
Его можно записать, двумя :
Или как 1000a + 100b + 10c + 0, или как 1000a + 100b + 10c + 5.
Число в обратном порядке тогда будет тоже одно из двух:
Или 100c + 10b + a, или 5000 + 100c + 10b + a.
Вычитаем из первого числа второе и получаем два случая:
1) 1000a+100b+10c - (100c+10b+a) = 999a+90b-90c = 4266
9(111a + 10b - 10c) = 4266 = 9*474
111a + 10b - 10c = 100a + 10(a + b - c) + a = 474
{ a = 4;
{ a + b - c = 7
4 + b - c = 7
b - c = 3
Варианты: (b = 9, c = 6); (b = 8, c = 5); (b = 7, c = 4); (b = 6, c = 3);
(b = 5, c = 2); (b = 4, c = 1); (b = 3, c = 0).
Решения: 4960, 4850, 4740, 4630, 4520, 4410, 4300.
Проверим какое-нибудь из решений:
4630 - 364 = 4266, все правильно.
2) 1000a+100b+10c+5 - (5000+100c+10b+a) = 999a+90b-90c-4995 = 4266
9(111a + 10b - 10c) = 4266 + 4995 = 9261 = 9*1029
111a + 10b - 10c = 1029
Здесь решения нет, потому что слева число трехзначное, а справа четырехзначное.
1.Найти радиус описанной окружности (R) для равнобедренного треугольника с основанием 10 см и боковой стороной 13 см
.
h = √(169 - 25) = √144 = 12 см.
S = (1/2)*10*12 = 60 см².
R = abc/(4S) = (13*13*10)/(4*60) = 169/24 ≈ 7,04167 см.
2.Найдите радиус вписанной окружности (r) для квадрата,периметр которого 16 см.
Сторона равна 16/4 = 4 см.
Радиус r = 4/2 = 2 см.
3.В прямоугольном треугольнике ABC катеты AB и BC равны соответственно 20 см и 21 см.Найти гипотенузу AC и косинус угла А
АС = √(20² + 21²) = √(400 + 441) = √841 = 29 см.
4.Найти высоту трапеции,основания которой 1 см и 5 см,боковая сторона 4 см.
Можно найти только в случае, если трапеция равнобокая.
h = √(4² - (5 - 1)/2)²) = √(16 - 4) = √12 = 2√3 см.