Дана прямая L: 3x - 5y + 30 = 0.
Находим точки пересечения её с осями координат.
Ось Ох: у = 0, 3х = -30, х = -30/3 = -10. Точка А (-10; 0).
Ось Оу: х = 0. 5у = 30, у = 30/5 = 6. Точка В (0; 6).
Для перпендикулярной прямой коэффициенты А и В прямой L меняются на -В и А. Получаем уравнение 5х + 3у + С = 0.
Для определения слагаемого С подставим координаты найденных точек А и В.
Для точки А: 5*(-10) + 3*0 + С = 0, отсюда С = 50.
Уравнение перпендикуляра через точку А: 5х + 3у + 50 = 0.
Для точки В: 5*0 + 3*6 + С = 0, отсюда С = -18.
Уравнение перпендикуляра через точку В: 5х + 3у - 18 = 0.
решение на фотографии
проще объяснить по тригонометрической окружности.
а) рисуем окружность, находим ось cosx и по ней отмечаем числовые значение (корень из 3)/2 (просто рисуем вертикальную линию). Если знаете таблицу синусов-косинусов углов в 30/45/60, то вспомните, что (корень из 3)/2 - это 30 градусов. и все: то, что в скобочка приравниваем к найденным углам (сначала П/6, потом -П/6).
б) с тангенсом посложнее объяснить.
я отмечаю тоже по окружности, хотя можно просто выучить эти значения с углами. корень из 3 - П/3.
Как я делаю: tgx= sinx/cosx. Отмечаем на оси синуса корень из трех (горизонтальную линию) и ведём к оси косинуса, в точку пересечения окружности и оси косинуса. в этой точке косинус равен 1. Вот и получается, что
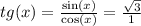
и проводим диагональ получившегося прямоугольника - так отмечаем нужные нам углы. снова приравниваем все, что внутри скобок, к этим углам и находим нужный.
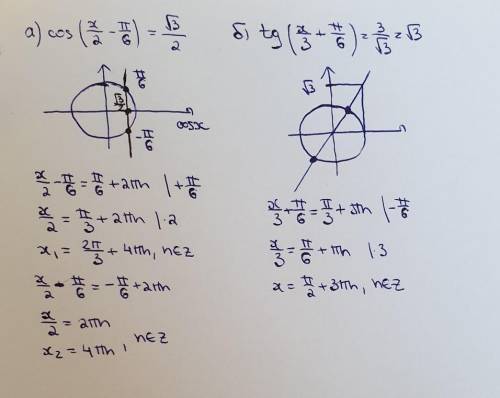
Выполняем умножение одночленов на многочлены:
83+5y-15=24y-27
Переносим все корни влево, все оставшееся - вправо (при этом меняя знаки на противоположные)
5y-24y=-27-83+15
Упрощаем:
-19y=-95
Решаем:
y=-95:(-19)
y=5
Проверка:
83+5*5-15=24*5-27
83+25-15=120-27
93=93