Пошаговое объяснение:
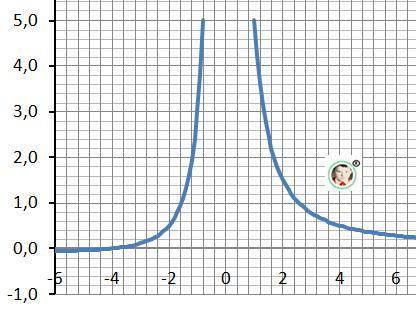
Рисунки с графиками функции в приложении.
1. Область определения х≠0
D(f)=(-∞;0)∪(0;+∞)
Вертикальная асимптота: х = 0.
2. Пересечение с осью ОХ
4 + х = 0
х = -4 - на втором рисунке
3. Знакопостоянство.
Отрицательна: y≤0, x=(-∞;4].
Положительна: y>0 x=(-4;0)∪(0;+∞).
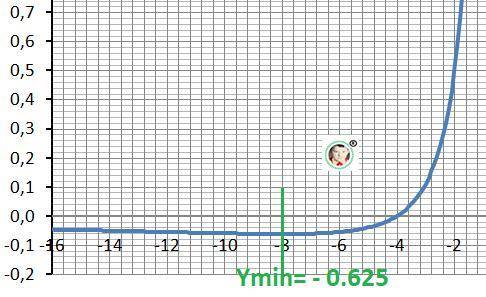
4. Экстремумы по первой производной.
f(x)' = -(x+8)/x³ = 0
x = -8 - точка экстремума
5. Локальный экстремум.
Минимум при х = - 8. Ymin = - 0.625.
6. Монотонность поведения.
Убывает: х=(-∞;-8)∪(0;+∞)
Возрастает: x = (-8;0).
7. Выпуклость по второй производной.
f(x)" = (2*x +24)/x⁴ = 0.
x = - 12.
8. Поведение.
Выпуклая: х=(-∞;-12).
Вогнутая: x=(-12;0)∪(0;+∞)
9. Наклонная (горизонтальная асимптота.
у = 0.
Например:
Чтобы умножить на 2 нужно сложить (+) большее число (Например число 5) два раза: 5*2=5+5=10
Чтобы умножить на 3 нужно сложить (+) большее число (Например число 5) три раза: 5*3=5+5+5=15
Чтобы умножить на 4 нужно сложить (+) большее число (Например число 5) четыре раза: 5*4=5+5+5+5=20
Чтобы умножить на 5 нужно сложить (+) большее число (Например число 5) пять раз: 5*5=5+5+5+5+5=25
Чтобы умножить на 6 нужно сложить (+) большее число (Например число 5) шесть раз: 5*6=5+5+5+5+5+5=30
Чтобы умножить на 7 нужно сложить (+) большее число (Например число 5) семь раз: 5*7=5+5+5+5+5+5+5=35
Чтобы умножить на 8 нужно сложить (+) большее число (Например число 5) восемь раз: 5*8=5+5+5+5+5+5+5+5=40
Чтобы умножить на 9 нужно сложить (+) большее число (Например число 5) девять раз: 5*8=5+5+5+5+5+5+5+5+5=45
2) 5+7+14=26 (ф)- вырезала оля всего
ответ 26 фигур