
В задаче не сказано какой формы будут клумбы - вот и задумался садовник. Рисунок к задаче в приложении.
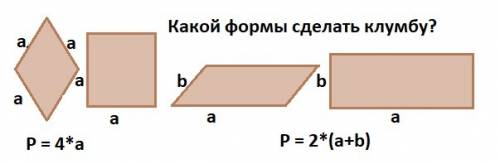
Если стороны равны - а , то это ромб или квадрат. Тогда периметр по формуле: Р = 4*а.
Если стороны разные: a и b, то это параллелограмм или прямоугольник и периметр по формуле: P = 2*(a + b).
1) а = b = 4 м. Р1 = 4*а = 4*4 = 16 м - периметр первой клумбы.
2) Р2 = 2*(6 + 4) = 2*10 = 20 м - периметр второй клумбы
3) Р3 = 2*(7 + 2) = 2*9 = 18 м - периметр третьей клумбы.
4) Р4 = 2*(5 + 3) = 2*8 = 16 м - периметр четвёртой клумбы.
И теперь длину изгороди на все четыре клумбы - сумма отдельных.
5) Р = 16+20+18+16 = 70 м на все четыре клумбы - ОТВЕТ
НОД (12; 20) = 4
НОД (27; 72) = 3 * 3 = 9
Пошаговое объяснение:
Наибольший общий делитель (НОД) двух чисел - это наибольшее число, на которое оба числа делятся без остатка.
1. НОД (12; 20)
Разложим на простые множители число 12 :
12 = 2 * 2 * 3
Разложим на простые множители число 20 :
20 = 2 * 2 * 5
Выберем одинаковые простые множители в обоих числах: 2, 2
Находим произведение одинаковых простых множителей и записываем ответ :
НОД (12; 20) = 2 * 2 = 4
2. НОД (27; 72)
Разложим на простые множители число 27 :
27 = 3 * 3 * 3
Разложим на простые множители число 72 :
72 = 2 * 2 * 2 * 3 * 3
Выберем одинаковые простые множители в обоих числах: 3, 3
Находим произведение одинаковых простых множителей и записываем ответ :
НОД (27; 72) = 3 * 3 = 9