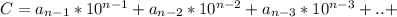
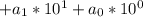 (1)
(1)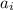 - некоторые коэффициенты, принимающие целые значения от 0 до 9 (0, 1, 2, 3,...9)
- некоторые коэффициенты, принимающие целые значения от 0 до 9 (0, 1, 2, 3,...9)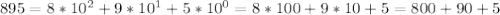
 (2)
(2)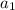 и
и 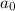
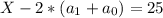
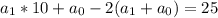
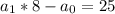 (3)
(3)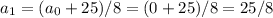 a_{1}=(a_{0}+25)/8=(9+25)=34/8
a_{1}=(a_{0}+25)/8=(9+25)=34/8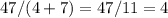 остаток 3.
остаток 3.
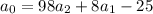
9.
а)250 ,300, 350
Каждое следующее число ряда больше на 50.
350 + 50 = 400.
400 + 50 = 450.
450 + 50 = 500.
ответ: 400, 450, 500.
б)400, 425, 450
Каждое следующее число ряда больше на 25.
450 + 25 = 475.
475 + 25 = 500.
500 + 25 = 525.
ответ: 475, 500, 525.
в)20, 40, 80
Каждое последующее число ряда больше предыдущего в два раза.
80 * 2 = 160.
160 * 2 = 320.
320 * 3 = 640.
ответ: 160, 320, 640.
г)800, 400, 200
Каждое последующее число ряда меньше предыдущего в два раза.
200 / 2 = 100.
100 / 2 = 50.
50 / 2 = 25.
д) 910, 820, 730.
Каждое последующее число ряда меньше на 90.
730 – 90 = 640.
640 – 90 = 550.
550 – 90 = 460.
ответ: 640, 550, 460.
е) 884, 775, 666.
Каждое последующее число ряда меньше на 109.
666 – 109 = 557.
557 – 109 = 448
448 – 109 = 339.
ответ: 557, 448, 339
Пусть объём бассейна равен 1, тогда время его заполнения до ремонта первым насосом – x, а вторым – y часов. Следовательно, 1/x - производительность первого насоса до ремонта, а 1/y - производительность второго насоса до ремонта. Зная, что бассейн до ремонта насосов заполняется за 8 часов, то составим первое уравнение: 8(1/x+1/y)=1, т.е. 8/x+8/y=1.
1,2(1/x) - производительность первого насоса до ремонта, а 1,6(1/y) - производительность второго насоса после ремонта. Зная, что бассейн после ремонта насосов заполняется за 6 часов, то составим второе уравнение: 6(12/x+16/y)=1, т.е. 7,2/x+9,6/y=1.
Решив совместно эти два уравнения , получаем : x=12, y=24.
Из найденных значений для x и y вычислим производительность первого насоса после ремонта: 1,2(1/x)=(1,2*1)/12=0,1
По формуле t=A/P найдём время наполнения бассейна при работе только первого насоса после ремонта: 1/0,1=10 ч.
ответ: 10 ч.