ответ: -∞.
Пошаговое объяснение:
Обозначим g(x)=e^(1/x)-1 и h(x)=arctg(x²)-π/2. По правилу Лопиталя, lim (x⇒∞) g(x)/h(x)=lim (x⇒∞) g'(x)/h'(x). Так как g'(x)=-1/x²*e^(1/x), а h'(x)=2*x/(1+x⁴), то g'(x)/h'(x)=-e^(1/x)*(1+x⁴)/(2*x³). Так как предел первого множителя при x⇒∞ равен -1, то искомый предел равен пределу дроби (1+x⁴)/(2*x³), взятому с обратным знаком. Разделив числитель и знаменатель дроби на x³, получим выражение (1/x³+x)/2. Очевидно, что предел этого выражения при x⇒∞ равен (0+∞)/2=∞, а потому искомый предел равен -∞.
Есть формула, которая выводится из основного тригонометрического тождества и которая связывает котангенс и синус.
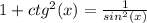
*чтобы её вывести, подели каждое слагаемое и сумму в основном тригонометрическом тождестве на синус в квадрате.
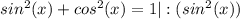
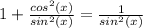
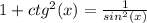
**аналогичная формула существует и для связи тангенса и косинуса.(только теперь нужно делить на косинус в квадрате).
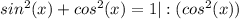
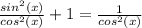
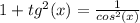
Итак, зная это выведем из формулы синус:
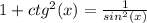
(возведём обе стороны выражения в "-1" степень, вследствие этого числители и знаменатели "перевернутся")
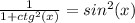
Тогда:
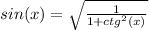
Подставляем исходное значение котангенса:
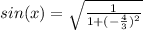
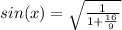

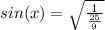
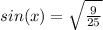
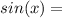 ±
±
Поскольку угол "x" лежит в четвёртой четверти по условию (от 3п/2 до 2п), а значения синусов в этой четверти отрицательные, следовательно:
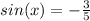
Формула косинуса двойного угла (1):

Выразим косинус из основного тригонометрического тождества (2):
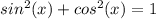
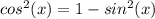
Подставим полученное выражение косинуса (2) в формулу косинуса двойного угла (1):
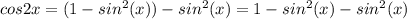
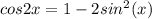
Подставим посчитанное ранее значение синуса в полученную формулу и найдем искомый косинус двойного угла:

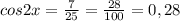
ответ: 0,28
б), г) заметим, что если перед ходом противника на поле (0, 0), (1, 2), (3, 3), (4, 5), (6, 6), (7, 8), (9, 9) или (10, 11) (запись (а, b) означает, что в одном столбце a минусов, в другом b), то он проигрывает. Это так, поскольку одним ходом нельзя перевести одно из этих положений в другое, а двумя можно. Значит, выигрывает первый, первым ходом он должен убрать минус из одного из столбцов, а остальными ходами либо выигрывать, либо сводить всё к выписанным комбинациям.