545. в) [4; 4.5]
546. б) (0,5; -2)
547. a) (2; 2)
548. в) (2; -4)
549. в) (1; 2)
550. a) (1; 5)
Пошаговое объяснение:
545.
{ x-4 ≥ 0 ⇒ x ≥ 4
{ 9-2x ≥ 0 ⇒ -2x+9 ≥ 0 ⇒ -2x ≥ -9 ⇒ x ≥ 4.5
x ∈ [4;4.5]
546.
{ x+y= -3/2
{ x-y= 2.5
2y= -4
y= -2
x-2= -3/2
x= 0.5
547.
{ 2x-y=2
{ x+2y=6│*2
{ 2x-y=2
{ 2x+4y=12
-5y= -10
y=2
2x-2=2
2x=4
x=2
548.
{ 7x+2y=6 │*5
{ -3x+5y= -26│*2
{ 35x+10y=30
{ -6x+10y=18
41x=82
x=2
14+2y=6
2y=6-14
2y= -8
y= -4
549.
{ -2x-y= -4
{-x+5y=9 │*2
-11y= -22
y=2
-2x-2= -4
-2x= -4+2
-2x= -2
x=1
550.
{ 6x+2y=16│*2
{ 2x-4y= -18
{ 12x+4y=32
{2x-4y= -18
14x=14
x=1
6+2y=16
2y=16-6
2y=10
y= 5
Ряд сходится, но не сходится абсолютно
Пошаговое объяснение:
Домножим каждый член ряда на 3, от этого сходимость не поменяется, так что с этого места считаем, что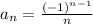 
.
Заметим, что ряд составленный из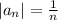 
является гармоническим рядом, который, как известно, расходится. Поэтому ряд не сходится абсолютно. Чтобы доказать просто сходимость, разобьем слагаемые попарно:
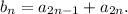
Заметим, что
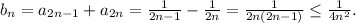Заметим, что ряд составленный из 
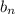сходится, так как он составлен из положительных членов и мажорируется сходящимся рядом 
Обозначим частичные суммы ряда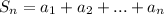 
.
Тогда в наших обозначения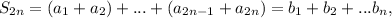 
а ряд из 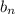сходится, значит 
имеет предел. Обозначим этот предел за 
. Для окончания доказательства, докажем что частичные суммы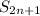 
тоже сходятся к a.
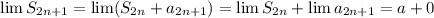, так как очевидно, что 
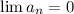. Итого, мы доказали, что у частичных сумм есть предел , значит ряд сходится по определению
Всё очень просто