Рисунок во вложении.
1. Нарисовать две прямые а и b.
2. Совместить сторону (катет) прямого угла угольника с прямой а, а к другой стороне (катету) приложить линейку.
3. Двигать угольник по линейке до прямой b.
4. Проверить, если та сторона, которая была совмещена с прямой а, совмещается, также, и с прямой b.
Если совмещается, то прямые параллельны, если нет - то не параллельны.
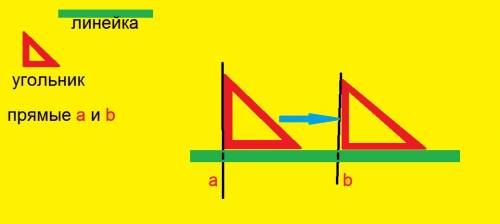
На рисунке видно, что сторона угольника не совместилась с прямой b, значит эти прямые не параллельны.
ответ: построение параллельных прямых неточное, a ∦ b.
При данной проверке подтвеждается правило параллельности прямых: " Если две прямые на плоскости перпендикулярны третьей прямой, то они параллельны."
В роли третьей прямой выступает линейка, а угольник проверяет, если углы пересечения прямых а и b с линейкой равны.
Расстояние от Ростова до логова Тугарина обозначим s.
Змей встретил Моисея на обратном пути в 18 верстах от логова. То есть, за время, пока Моисей верст, Змей пролетел s+18.
(s-18)/m=(s+18)/z
А Юлия в 25 верстах от логова.
(s-25)/u=(s+25)/z
А Моисей встретил Юлия уже в 8 верстах.
(s-8)/u=(s+8)/m
Из 3 уравнения выразим u через m и s
u=m*(s-8)/(s+8)
Подставим во 2 уравнение
(s+25)/z=(s-25)(s+8)/(m(s-8))
m(s-8)(s+25)=z(s-25)(s+8)
Но из 1 уравнения
m(s+18)=z(s-18)
Делим одно уравнение на другое.
(s^2+17s-200)/(s+18)=(s^2-17s-200)/(s-18)
(s-18)(s^2+17s-200)=(s+18)(s^2-17s-200)
s^3-s^2-706s+3600=s^3+s^2-706s-3600
2*3600=2s^2
s^2=3600
s=60 верст от Ростова до логова Тугарина.