Відповідь:
14 часов
Покрокове пояснення:
Для решения задачи сперва нужно определить количество времени за которое бассейн наполняется через 2 трубы.
Для этого находим продуктивность работы каждой из труб за 1 час.
Поскольку вся работа равна 1, получим.
1/12 продуктивность работы первой трубы за час.
1/24 продуктивность работы второй трубы за час.
1/12+1/24=3/4=1/8. Продуктивность работы двух труб за час вместе.
Находим количество работы для второй трубы за 9 часов.
Получим.
1/24*9=3/8.
Находим количество работы выполненное первой трубой.
1-3/8=5/8.
Находим период работы двух труб вместе.
5/8 / 1/8=5/8*8/1=40/8=5 часов.
Находим период наполнения.
5+9=14 часов.
Пошаговое объяснение:
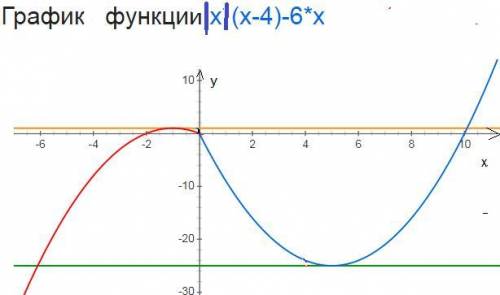
при х≥0 IxI=x
y=x(x-4)-6x=x²-4x-6x=x²-10x
при х<0 IxI=-x
y=-x(x-4)-6x=-x²+4x-6x=-x²-2x
найдем точки пересечения графиков x²-10x=-x²-2x; 2x²-8x=0; 2x(x-4)=0
x1=0;x2=4
y=x²-10x это парабола, вершина х0=-b/2a=10/2=5; y0=25-50=-25
вершина (5;-25) точки пересечения с осью ОХ x(x-10)=0; x1=0;x2=10
y=-x²-2x это парабола, вершина х0=-b/2a=-2/2=-1; y0=-1+2=1
вершина (-1;-1) точки пересечения с осью ОХ -x(x+2)=0; x1=0;x2=-2
из графика видно что прямая у=к будет иметь с графиком ровно две общие точки если будет проходить через вершины
у=1; y=-25
⇒ k={1;-25}