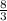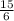.
. Готово.
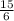и , где числитель дроби — общее число бросков, а ее знаменатель — число попаданий. Видно, что при одинаковом числе попаданий, второй баскетболист совершил меньше бросков, а значит и его результат лучше.
Возьмем, к примеру, кубик со стороной 
. Его объем равен 
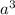. Если мы сторону кубика увеличим в n раз, то сторона кубика станет равной 
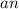. Тогда его объем будет равен 
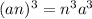. Видно, что если поделить объем кубика со стороной на объем кубика со стороной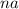 
, то получим 
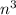. Именно во столько раз изменится объем.
Аналогично можно проделать рассуждения для шара. При увеличении радиуса в n раз объем шара увеличится в 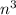раз.
Для параллелепипеда с увеличением всех сторон в n раз его объем увеличится в 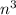раз.
Вообще, для тела произвольной формы эта закономерность сохраняется. Нестрого говоря, любое тело можно разбить на кубики (чем меньше сторона кубика, тем точнее можно описать произвольное тело), и, поскольку у каждого кубика объем увеличивается в 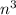раз, то и объем всего тела увеличится также.
