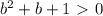при всех b (можно, скажем, для доказательства этого проверить, что дискриминант отрицателен);
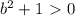при всех b - очевидно. Поэтому неравенство равносильно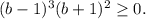
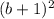всегда больше либо равно нуля, поэтому может повлиять на знак произведения только там, где обращается в ноль, а обращается оно в ноль при b= - 1; это значение b входит в ответ. При прочих b эта скобка не влияет на знак произведения и поэтому может быть отброшена. Остается скобка 
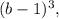которая имеет тот же знак, что и (b-1).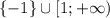
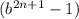совпадает со знаком выражения (b-1), а знак выражения 
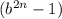- со знаком 
После этого перестаешь бояться выражений вида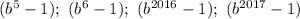 
и так далее
Надо доказать: (a+b)/2b<a/b , умножив на положительный знаменатель: получаем (a+b)<2a. Вычитая а из обоих частей
a>b, т.е. неравенство равносильно данному b<a