Пошаговое объяснение:
9/15 на 3 сокращаем = 3/5
14/63 на 7 = 2/9
25/48 и 13/24
13/24 на 2 = 26/48
25/48 ∠26/48
7/9 на 7 и 5/7 на 9
49/63 больше 45/63
3.
3/10 +5/12 Обе дроби на 5 умножаем
15/50 + 25/50
40/50=4/5
13/24 - 7/16 на 2 и на 3
26/48 - 21/48
5/48
1 4/15 + 3 7/25
19/15 + 82/25 на 5 и на 3 умножаем
95/75 + 246/75
341/75= 4 41/75
9 11/12 - 5 3/8
119/12 - 43/8 на 2 и на 3
238/24 - 129/24 = 109/24= 4 15/24
4.
7 2/5 - 2 9/20
37/5 - 49/20 на 4
148/20 -49/20= 99/20=4 19/20
7 2/5 +4 19/20= 37/5 + 99/20 на 4
148/20 +99/20=247/20= 12 7/20
Пошаговое объяснение:
1) Сократите дробь

2) Сравните дробь
Чтоб сравнить дроби с разными знаменателями надо привести их к одному знаменателю
а) 25/48 и 13/24
48 = 2 * 24
Значит общий знаменатель 48
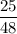 и
и 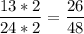
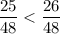
значит
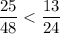
б)  и
и 
общий знаменатель 9*7= 63
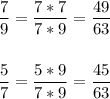
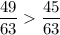
значит
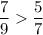
3) Вычислите
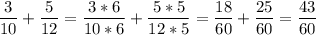
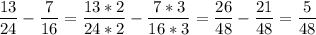
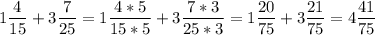
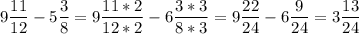
4) Найдем массу цинка
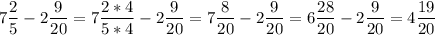 кг
кг
Теперь найдем массу сплава :
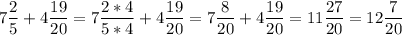 кг масса сплава
кг масса сплава
5) Решить уравнение
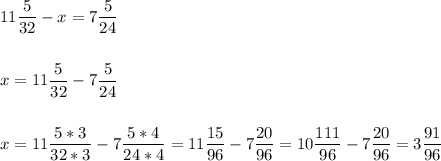

6. Все поле это 1 целая
Сложим части которые вспахали три трактора :
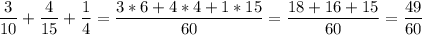
Найдем какую часть вспахал четвертый трактор :
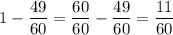
Четвертый трактор вспахал 11/60 площади поля
7.
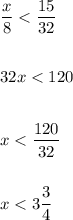
Значения х при , которых верно равенство будут : 1; 2; 3
1) а=1
2) a≠1
найдем дискриминант
чтобы были решения нужно чтобы D≥0
теперь найдем корни уравнения
первый корень
при этом а≠1
решим неравенство
найдем нули числителя
где a≤1.25
2a-4≥0
a≥2
Значит числитель нулю при а≤1,25 не равен
расставим знаки
_____-__________+_______
1 1,25
Значит а∈(1;1.25]
второй корень
при а≠1 решим это неравенство
найдем нули числителя
где 4-2а≥0; a≤2
расставим знаки
___-______+_____+_____
-1 1 1,25
при a∈[-1;1)∪(1;1.25]
теперь найдем пересечение решений
a=1. a∈(1;1.25] a∈[-1;1)∪(1;1.25]
ответ a∈[1;1.25]