190 прямых
Пошаговое объяснение:
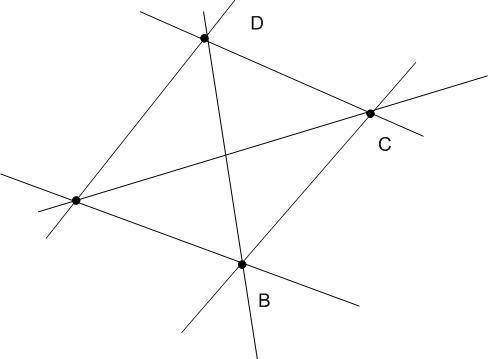
попробуем построить, ну, например для 4-х точек (см.рис).
Прямая проходит через каждые две точки. Т.е. нужно посчитать сколько различных пар точек можно выбрать из 4-х точек. Это - известная в комбинаторике формула для подсчета числа сочетаний (именно сочетаний, а не размещений, потому, что прямая АВ и прямая ВА - одна и таже прямая). Подсчитаем для 4-х точек:
C₄²=4!/(4-2)!4!=4!/(2!*2!)=3*4/2=6;
и действительно видим 6 прямых. Тогда для 20 точек:
C₂₀²=20!/((20-2)!2!)=19*20/2=190.
3x + 6
Пошаговое объяснение:
Прямая пройдёт через точку (2 ; 0). Значит в этой точке она пересечёт ось OX.
Параллельность прямых будет задаваться условием, что y = 3x + k, где k - коэффициент, который нужно определить. 3x - отвечает за такой же угол наклона между прямой и осью OX.
Значит 0 = 3х - k. Подставив x = 2, получим, что k = 6.
Значит уравнение примет вид: 3x + 6.
(Для понимания постройте прямую, данную в примере и прямую, которую мы получили в ответе. Вы заметите, что коэффициенты k - координата точки пересечения оси OY, а коэффициенты при X (3x) - коэффициент наклона примой к оси OX).