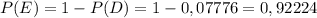. Условие, что выражение равно единице, можно записать так:
(100 + n)k(100 - n)l = 100k + l. Так как правая часть четна, то и левая часть должна быть четна, значит, n четно. Аналогично, левая часть делится на 5, значит, n делится на 5. Значит, n делится на 10. Можно перебрать все 9 возможных вариантов: n = 10, 20, ..., 90. Например, если n = 10, то левая часть делится на 11, что невозможно.Можно обойтись без перебора: пусть n не делится на 25. Тогда числа 100 - n и 100 + n тоже не делятся на 25. Значит, пятерка входит в разложение левой части на простые множители ровно k + l раз. Но она входит в разложение правой части 2(k + l ) раз -- противоречие. Итак, n делится на 25. Аналогично доказывается, что n делится на 4. Но тогда n делится на 100, что невозможно, ибо 0 < n < 100.
ответ: a) 0,3456
б) 0,68256
в) 0,92224
Пошаговое объяснение:
При решении используется формула Бернулли.
Вероятность вытянуть изделие высшего сорта p = 40% = 0,4
Вероятность не вытянуть изделие высшего сорта q = 1 - p = 1 - 0,4 = 0,6
а) A: "из пяти случайно отобранных изделий 2 высшего сорта"
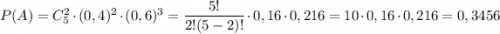
б) B: "из пяти случайно отобранных изделий не более 2 высшего сорта"
Не более двух - это 0, 1 или 2 изделия высшего сорта
C: "из пяти случайно отобранных изделий 1 высшего сорта"
D: "из пяти случайно отобранных изделий 0 высшего сорта"
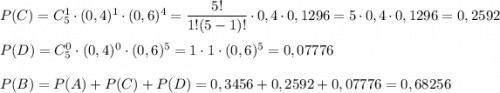
в) E: "из пяти случайно отобранных изделий хотя бы одно высшего сорта"
Найдём вероятность события E через противоположное событие D.