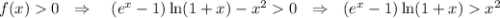Рассмотрим функцию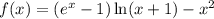 
.
Область определения функции: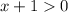 
откуда 
.
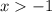Исследуем функцию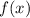 
на монотонность. Ищем производную функции
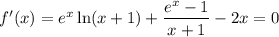
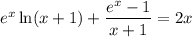
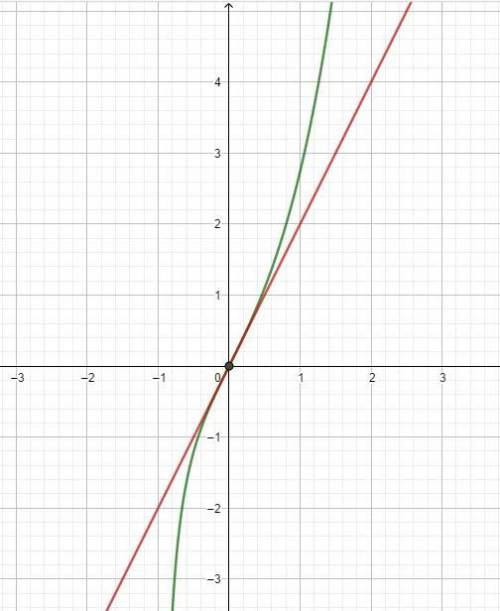
Строим график функции стоящую слева в уравнении - возрастающая (на области определения) и прямую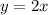 
. Графики пересекаются только в одной точке (0;0).
(-1)___-____(0)_____+____
При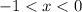 
производная отрицательная, а при 
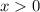- положительная. Следовательно, функция 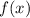на промежутке 
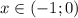убывает, а на пром. 
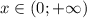- возрастает. Значит, в точке 
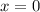функция имеет максимум, который равный 0
Следовательно, функция 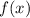всюду положительна на области определения и кроме точки 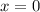, получаем
