Математика: Прислів я приказки загадки про грунт

Прислів'я приказки загадки про грунт

👇

Увидеть ответ

Ответ:

Викa2003648219

17.07.2020

До першого грому земля не розмерзнеться
Один ллє, другий п'є, третій росте. (дощ, ґрунт, рослина)

Що лицюєм на всі боки,

А воно нове щороку(ґрунт)

4,7(2 оценок)

Ответ:

Tyan789

17.07.2020

До першого грому земля не розмерзнеться.

Як почав орати, то в сопілку не грати.

Глибше орати — більше хліба мати.

Добре ґрунт угноїш - урожай потроїш.

Хто про землю дбає, вона тому повертає.

Поле працю любить.

Землю гріх ображати, бо вона наша мати.

На чорній землі білий хліб родить.

На добрій землі що не посієш, те й вродить.

Жита ростуть, як з води йдуть.

Ялова земля не нагодує, а сама їсти просить.

4,7(85 оценок)

Открыть все ответы

Ответ:

MIshaDo

17.07.2020

6/Задание № 1:

Сколько двузначных чисел, которые уменьшаются в 13 раз при отбрасывании последней цифры?

РЕШЕНИЕ: Пусть это число АВ=10a+b. При отбрасывании последней цифры возникает число A=a. Двузначное число в 13 раз больше однозначного, значит:

10a+b=13a

b=3a

Так как а и b цифры, то они должны быть целыми числами от 0 до 9, при чем а не совпадает с нулем, так как исходное число двухзначное.

Если а=1, то b=3 - число 13

Если а=2, то b=6 - число 26

Если а=3, то b=9 - число 39

Если а=4 и более, то b=12 и более - b не соответствует цифре

ОТВЕТ: 3 числа

4,8(11 оценок)

Ответ:

OlgaStarikova

17.07.2020

Попробуем понять, что от нас хотят? Поэтому разберёмся для начала, что такое [a]? Как сказано, это наибольшее целое число, не больше а, т.е. меньше или равно. [a] ≤ a.
А чтоб совсем понятно стало, рассмотрим примеры.
Например, а = 6,37, значит, [a] = 6; а = 0,88 и [a] = 0; a = 1,0 и [a] = 1.
Т.о. просто отбрасывается дробная часть.
Это для положительных чисел, а для отрицательных? Здесь отбрасывание дробной части не даёт результата.
Например, a = -6,37 и, если [a] =-6, то -6 ≥ -6,37, т.е. [a] > a, что расходится с условием. Поэтому, [a] = -7 (!)
a = -2,03 и [a] = -3; a = -0,88 и [a] = -1; a = -1,0 и [a] = -1.
Т.о., если есть дробная часть, то она отбрасывается и производится вычитание единицы.

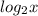Теперь разбираемся с условием, вероятность которого необходимо вычислить: [log_2 x] = [log_2 y]

. Равенство будет выполняться. если два случайных числа будут попадать в одинаковые интервалы, дающие при получении наибольшего целого, не превосходящее само число.

Какой интервал надо разбивать? Разбивать надо интервал (0, 1), но так, чтобы log_2x

в граничных точках давал целые значения. Причём в интервале (0, 1) логарифм по основанию 2 меньше нуля.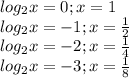
Например:
$log_2x = 0; x =1 \\ log_2x = -1; x = \frac{1}{2} \\ log_2x = -2; x = \frac{1}{4} \\ log_2x = -3; x = \frac{1}{8}$

Отсюда, становятся понятны интервалы (справа налево):
от 1 до 1/2 - здесь [log_2x]=-1

от 1/2 до 1/4 - здесь [log_2x]=-2

от 1/4 до 1/8 - здесь [log_2x]=-2

И т.д., интервал всё время сокращается в два раза.

Наконец, переходим непосредственно к вероятности. Вероятность выбора числа х из интервала от 1 до 1/2 равна отношению длины этого интервала к общей длине. Длина интервала = 1/2, общая длина = 1. Вероятность равна 1/2. Точно такая же вероятность случайного выбора числа у из этого же интервала - 1/2. Т.к. события не зависят друг от друга, то вероятность одновременного попадания обоих чисел в этот интервал равна 1/4 = 1/2 * 1/2.
Аналогично вычисляются вероятности попадания в остальные интервалы. Так вероятность попадания чисел х и у в интервал от 1/2 до 1/4 равна: 1/16 = 1/4 * 1/4. Ширина интервала равна 1/4, значит, и вероятности каждого события равны 1/4.
Вероятность попадания в третий интервал от 1/4 до 1/8 равна:
1/64 = 1/8 * 1/8. И т.д.
Стал ясен алгоритм вычисления нашей вероятности. Надо для бесконечного числа интервалов вычислить вероятность совместного попадания двух чисел, а затем всё просуммировать.

А вот здесь нам в бесконечных вычислениях геометрическая прогрессия. Замечаем, что первый член равен 1/4, а знаменатель прогрессии 1/4. Поэтому, мы без проблем найдём сумму бесконечно убывающей геометрической прогрессии.

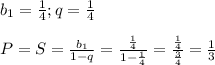
$b_1 = \frac{1}{4}; q = \frac{1}{4} \\ \\ P = S = \frac{b_1}{1-q} = \frac{ \frac{1}{4} }{1- \frac{1}{4} } = \frac{ \frac{1}{4} }{\frac{3}{4} } = \frac{1}{3}$

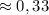Итак, вероятность оказалась равно 1/3, или $\approx 0,33$ .