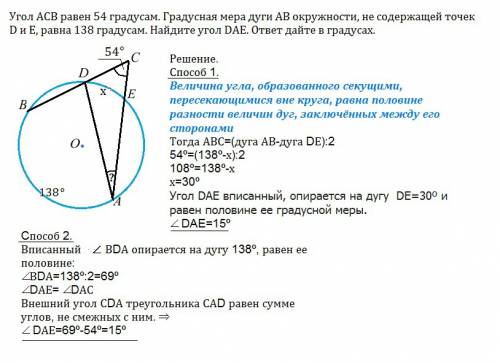
Угол ACB равен 54 градусам. Градусная мера дуги АВ окружности, не содержащей точек D и Е, равна 138 градусам. Найдите угол DAE. ответ дайте в градусах.
----------
Скорее всего, эта задача дается с готовым рисунком.
Угол АСВ образован секущими ВС и АС. пересекающим окружность с центром О в точках D и E
Решение.
Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами
Тогда АВС=(дуга АВ-дуга DЕ):2
54º=(138º-х):2
108º=138º-х
х=30º
Угол DAE вписанный, опирается на дугу DЕ=30º и равен половине ее градусной меры.
∠ DAE=15º
Cпособ 2.
Вписанный угол ВDА опирается на дугу 138º, равен ее половине:
∠ВDА=138º:2=69º
∠DАЕ= ∠DАС
Внешний угол СDА треугольника САD равен сумме углов, не смежных с ним. ⇒
∠ DАЕ=69º-54º=15º
x² - (y² + 4y +4) + 4=0,
х² - (у+2)² = -4 разделим на -4:
Это уравнение гиперболы, повёрнутой на 90 градусов с центром в точке (0;-2).
а = в = 2,
с = √(а²+в²) = 2√2.
Координаты фокусов: F1(0; 2√2-2 = 2(√2-1) ≈ 0,828427).
F2(0; 2√2+2 = 2(√2+1) ≈ 4,828427.
вершин: А1(0; 0).
А2(0; -4).
центра:(0;-2).
Уравнения асимптот: у = х - 2,
у = -х -2.