№829
1)Для каждого выражения под модулем уравнении допускаем случаи, когда соотв. выражение: ≥0 или <0, решаем получившиеся уравнения:
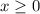
или:
0≤x/\x<∞
Получаем уравнение:
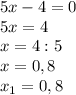
x<0
Получаем уравнение:
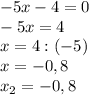
2)x≥0
Получаем уравнение:
17x/10-51/10=0 |*10
17X-51=0
17x=51
x=51:17
x=3
x1=3
x<0
Получаем уравнение:
-17x/10-51/10=0 |*10
-17x-51=0
-17x=51
x=51:(-17)
x= -3
x2= -3
3)y≥0
Получаем уравнение:
15y/2-15=0 | *2
15y-30=0
15y=30
y=30:15
y=2
y1=2
y<0
Получаем уравнение:
-15y/2-15=0 | *2
-15y-30=0
-15y=30
y=30:(-15)
y= -2
y2= -2
Пошаговое объяснение:
Решение.
Формула работы: А = р·t , где р - производительность , t - время , А - работа ⇒ р = А : t .
Если 1 насос наполняет 1/3 часть бассейна за 4 часа , то его производительность (скорость работы за единицу времени) равна
р₁=1/3 : 4=1/12 части бассейна в час .
Если 2 насос опустошает 1/4 часть бассейна за 4 часа , то его производительность равна р₂=1/4 : 4=1/16 части бассейна в час .
Так как 1 насос наполняет, а 2 насос опустошает бассейн, то их совместная производительность равна разности р₁ - р₂ .
р = р₁ - р₂ = 1/12-1/16 = 4/48 - 3/48 = 1/48 (части бассейна в час)
Вся работа принимается за 1, тогда t = A:p = 1:(1/48) = 48 часов .
ответ: 48 часов .
х*5/12+х/2+300=х
х=3600