Турист за два дня км пути. в первый день он шёл 7 часов , а во второй день 4 часа . сколько километров пути он в первый день и сколько во второй , если всё время шёл с одинаковой скоростью

👇

Ответ:

ENOT234u

22.12.2020

В сумме он шёл 7+4=11 часов. То есть скорость была 55/11=5 км/час. В 1 день пройдено 5*7=35 км, во второй 5*4=20 км. Проверка 25+20=55 км - верно!

ответ: 1 день 35 км, 2 день 20 км.

4,8(86 оценок)

Открыть все ответы

Ответ:

milashenko005

22.12.2020

Пошаговое объяснение:

Школьные Знания.com

Какой у тебя вопрос?

5 - 9 классыМатематика 5+3 б

1)Площадь прямоугольника равна 18 см2.Какими могут быть длины его сторон?Назовите 3 варианта.Найдите периметр каждого из трех названных прямоугольников

2)Площади пряямоугольника равны 36см2.Какими могут быть их периметры?Рассмотрите все возможные варианты.

3)Какой из прямоугольников,имеющих площадь 36 см2 имеет наименьший периметр?

Отметить нарушение Энциклопеди 20.01.2013

ответы и объяснения

vary02

Vary02 Хорошист

Первая задача:

1) 9х2=18 см2 Р=(9+2) х2=22 см

2) 6х3=18 см2 Р= (6+3) х2=18 см

3) 18х1 =18 см2 Р=(18+1)х2=38 см

Вторая задача:

1) (36+1)х2=74 см стороны 36 и 1 см

2) (18+2)х2=40 см стороны 18 и 2 см

3) (12+3)х2=30 см стороны 12 и 3 см

4) (9+4)х2=26 см стороны 9 и 4 см

5) (6+6)х2=24 см стороны 6 и 6 см

Третья задача:

Прямоугольник со сторонами 6см и 6 см имеет наименьший периметр

4,6(68 оценок)

Ответ:

эмилисенок2

22.12.2020

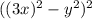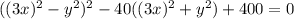Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: $((3x)^{2}-y^{2})^{2}$ ; В следующих двух слагаемых вынесем общий множитель "40": $40(9x^{2}+y^{2})=40((3x)^{2}+y^{2})$ ; В итоге получим следующее уравнение: $((3x)^{2}-y^{2})^{2}-40((3x)^{2}+y^{2})+400=0$ . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. 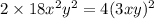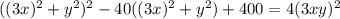Пусть в первой скобке вместо $(3x)^{2}-y^{2}$ будет стоять $(3x)^{2}+y^{2}$ ; Это приведет к тому, что придется убавить $2\times 18x^2y^2=4(3xy)^{2}$ ; В итоге: $((3x)^{2}+y^{2})^{2}-40((3x)^{2}+y^{2})+400= 4(3xy)^{2}$ ; Слева стоит квадрат суммы. 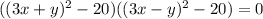Уравнение примет вид: $((3x)^{2}+y^{2}-20)^{2}=(6xy)^{2} \Leftrightarrow ((3x)^{2}+y^{2}-20+6xy)((3x)^{2}+y^{2}-20-6xy)=0$ ; Сворачивая еще раз: $((3x+y)^{2}-20)((3x-y)^{2}-20)=0$ ; Получаем серию прямых: $\pm 3x+\sqrt{20},\; \pm3x-\sqrt{20}$ ; А теперь приступим к рассмотрению первого уравнения.

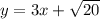Это уравнение задает круг с центром в точке (0, 0) и радиусом $\sqrt{2}$ ; Рассмотрим прямую $y=3x+\sqrt{20}$ ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 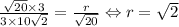$\frac{\sqrt{20}\times 3}{3\times 10\sqrt{2}}=\frac{r}{\sqrt{20}} \Leftrightarrow r=\sqrt{2}$ ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 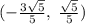$(-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5} } )$ ; Ну а все решения:

$(\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5})$