Раскрываем модуль по определению
Если
(x/2)-(2/x) ≥0, то | (x/2)-(2/x)|=(x/2)-(2/x)
y=(1/2)· (( x/2)-(2/x)) + (x/2)+(2/x)= (3/2)(x/2)+(1/2)(2/x)=(3x/4)+(1/x)
Если
(x/2)-(2/x) <0, то | (x/2)-(2/x)|= - (x/2)+(2/x)
y=(1/2)· (-(x/2)+(2/x)) + (x/2)+(2/x)= (1/2)(x/2)+(3/2)(2/x)=(x/2)+(3/x)
Так как
(x/2)-(2/x) ≥0 ⇒ (x²-4)/x≥0 ⇒ при x∈[-2;0)U([2;+∞)
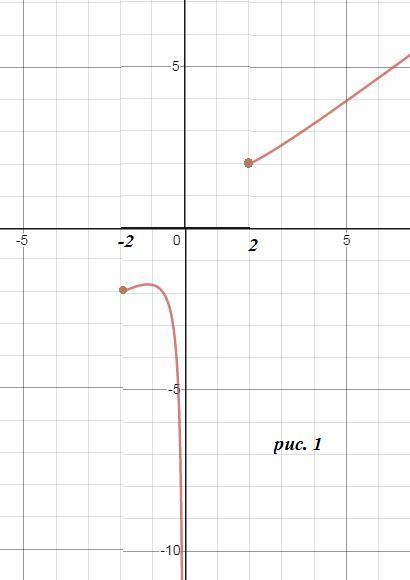
строим график y=(3x/4) + (1/x) на [-2;0)U([2;+∞)
рис. 1
(x²-4)/x < 0 ⇒ при x∈ (-∞;-2)U(0;2)
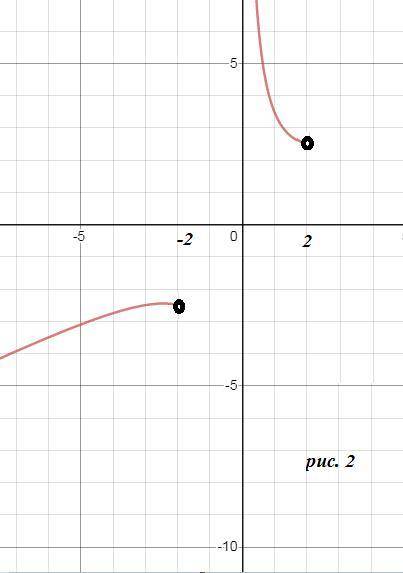
на (-∞;-2)U(0;2) строим график y=(x/2)+(3/x)
рис. 2
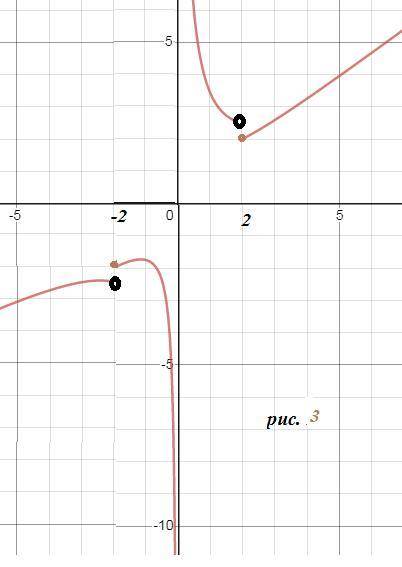
Окончательный график рис. 3
А(10,5) и В(6,3) надо найти длину отрезка АВ .т.А лежит правее,чем т.В,поэтому надо 10,5-6,3=4,2 получим расстояние между А и В.То же самое с отрицательными числами Р(-5,8) и М (-3,2). т.М лежит правее,значит -3,2-(-5,8)=-3,2+5,8=5,8-3,2=2,6 .если что не понятно,напиши.
__0___|__||___|___|_|||_|
0,63 1 2 2,51 3,35 4 4,85
здесь большой точности не будет,все приблизительно,особенно когда есть сотые доли числа.