Пусть все 290 слагаемых равны по 2. Тогда их сумма равна 290·2=580, что меньше 2020. Значит, среди слагаемых есть число, большее 2.
Пусть каждое из 290 слагаемых равно по 2 или по 3. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·3=870, что меньше 2020. Значит, среди слагаемых есть число, большее 3.
Пусть каждое из 290 слагаемых равно по 2, по 3 или по 5. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·5=1450, что меньше 2020. Значит, среди слагаемых есть число, большее 5.
Пусть каждое из 290 слагаемых равно по 2, по 3, по 5 или по 7. Тогда максимальная сумма, даваемая с таких слагаемых равна 290·7=2030. Это больше, чем 2020, значит такой вариант можно рассматривать далее.
Максимальная сумма получается при суммировании 290 чисел, каждое из которых равно по 7. Как видно, максимальная сумма больше требуемой на 10. Тогда, можно уменьшить некоторые слагаемые в этой сумме. Например, уменьшить 2 слагаемых на 5. Получим сумму вида:
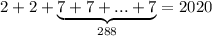
Наибольшим слагаемым является число 7.
ответ: 7
Пусть его скорость была -Хкм/ч.
Первый за 2 часа проехал 16*2=32 км,
что бы его догнать нужно 32/(Х-16) часов.
Второй за 1 час проехал 10 км,
что бы догнать второго нужно 10/(Х-10) часов.
Разница в гонке между ними известно по условию.
Состовляем уравнение
32/(Х-16)-10/(Х-10)=4,5
32Х-320-10Х+160=4,5(Х-10)(Х-16) при Х?10 и Х?16
22Х-160=4,5(Х?-26Х+160)
4,5Х?-139Х+880=0
Д=59?
Х1=(139+59)/9=22
Х2=(139-59)/9=8.(8)
Так как Х2<10 то это не может быть решением,
так как он никогда не догнал бы даже второго велосипедиста.
Получаем ответ при Х=22км/ч
ответ: 22 км/ч
Пошаговое объяснение:
2) 7 + 5 = 12 см/м скорость сближения мурашек
3) 12 * 60 сек (1 мин = 60 с) = 720 см проползут за 1 минуту
4) 1000 см (это 10 метров) - 720 см = 280 см = 2,8 метра будет между ними через 1 минуту
1) 3 + 2 = 5 часов был в пути
2) 70 * 5 = 350 км преодолел поезд