Есть формула, которая выводится из основного тригонометрического тождества и которая связывает котангенс и синус.
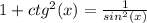
*чтобы её вывести, подели каждое слагаемое и сумму в основном тригонометрическом тождестве на синус в квадрате.
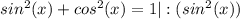
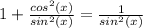
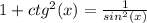
**аналогичная формула существует и для связи тангенса и косинуса.(только теперь нужно делить на косинус в квадрате).
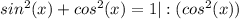
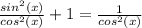
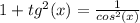
Итак, зная это выведем из формулы синус:
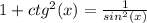
(возведём обе стороны выражения в "-1" степень, вследствие этого числители и знаменатели "перевернутся")
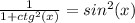
Тогда:
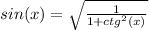
Подставляем исходное значение котангенса:
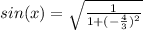
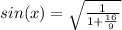

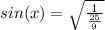
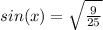
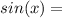 ±
±
Поскольку угол "x" лежит в четвёртой четверти по условию (от 3п/2 до 2п), а значения синусов в этой четверти отрицательные, следовательно:
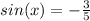
Формула косинуса двойного угла (1):

Выразим косинус из основного тригонометрического тождества (2):
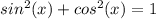
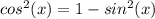
Подставим полученное выражение косинуса (2) в формулу косинуса двойного угла (1):
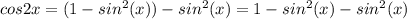
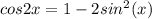
Подставим посчитанное ранее значение синуса в полученную формулу и найдем искомый косинус двойного угла:

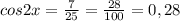
ответ: 0,28
Линейные уравнения ах = b, где а ≠ 0; x=b/a.
Пример 1. Решите уравнение – х + 5,18 = 11,58.
– х + 5,18 = 11,58;
– х = – 5,18 + 11,58;
– х = 6,4;
х = – 6,4.
ответ: – 6,4.
Пример 2. Решите уравнение 3 – 5(х + 1) = 6 – 4х.
3 – 5(х + 1) = 6 – 4х;
3 – 5х – 5 = 6 – 4х;
– 5х + 4х = 5 – 3+6;
– х = 8;
х = – 8.
ответ: – 8.
Пример 3. Решите уравнение .
. Домножим обе части равенства на 6. Получим уравнение, равносильное исходному.
2х + 3(х – 1) = 12; 2х + 3х – 3 =12; 5х = 12 + 3; 5х = 15; х = 3.
ответ: 3.
Пример 4. Решите систему
Из уравнения 3х – у = 2 найдём у = 3х – 2 и подставим в уравнение 2х + 3у = 5.
Получим: 2х + 9х – 6 = 5; 11х = 11; х = 1.
Следовательно, у = 3∙1 – 2; у = 1.
ответ: (1; 1).
Замечание. Если неизвестные системы х и у, то ответ можно записать в виде ко
Пошаговое объяснение:
надеюсь правильно
2) 16 : 4 = 4 (дж)
ответ:4 джемпера