1) 0,5 · (-9)⁴ + 1,1 · (-9)³ - 28 = 0,5 · 9⁴ - 1,1 · 9³ - 28 =
= 9³ · (0,5 · 9 - 1,1) - 28 = 9³ · (4,5 - 1,1) - 28 =
= 9³ · 3,4 - 28 = 729 · 3,4 - 28 = 2478,6 - 28 = 2450,6
2) 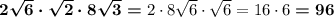
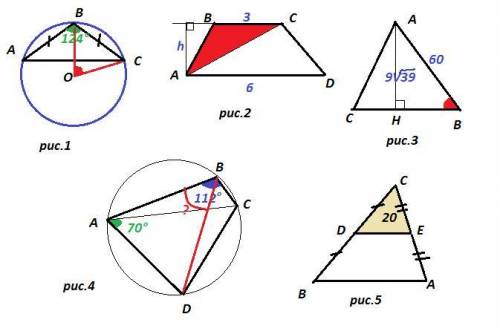
3) рис. 1
ΔABC - равнобедренный, AB = BC, ∠ABC = 124°
⇒ ∠A = ∠BCA = (180° - ∠ABC) : 2 = (180° - 124°) : 2 = 28°
∠A - вписанный в окружность. равен половине центрального угла ∠BOC, который опирается на ту же дугу, что и ∠A
∠BOC = 2∠A = 2 · 28° = 56°
4) рис. 2
Трапеция ABCD, AD║BC, AD = 6, BC = 3, S = 27
У ΔABC и трапеции ABCD одинаковая высота h, которую можно найти из формулы площади трапеции :
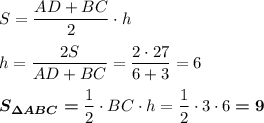
5) рис. 3
ΔABH : ∠AHB=90°, AB=60, AH = 9√39. Теорема Пифагора
BH² = AB² - AH² = 60² - (9√39)² = 3600 - 3159 = 441
BH = √441 = 21
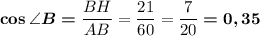
6) рис.4
∠ABC - вписанный, равен половине дуги, на которую опирается.
⇒ ∪ ADC = 2∠ABC = 2 · 112° = 224°
∠CAD - вписанный, равен половине дуги, на которую опирается.
⇒ ∪ DC = 2∠CAD = 2 · 70° = 140°
∪ AD = ∪ ADC - ∪ DC = 224° - 140° = 84°
∠ABD - вписанный, равен половине дуги, на которую опирается.
⇒ ∠ABD = ∪ DC : 2 = 84° : 2 = 42°
7) рис.5
Средняя линия треугольника отсекает от него подобный треугольник, площадь которого в 4 раза меньше площади большого треугольника
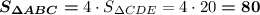
1.Найдите двадцать пятый член арифм. прогрессии (аn) если а1=16; d=4
а25=а1+24д=16+24*4=16+96=112
2. найдите сумму первых двенадцати членов арифм. прогрессии если а1=4; a12=26
S12=(а1+а12)/2*12=(4+26)/2*12=180
3. найдите сумму первых сорока членов последовательности (an); заданной формулой an=3n+2
а1=3*1+2=5
а40=3*40+2=122
S40=(а1+а40)/2*40=(5+122)/2*40=2540
4. является ли число -38 членом арифметической прогрессии 18; 4; ..
а1=18
а2=4
д=4-18=-14
18-14*(n-1)=-38
18-14n+14=-38
-14n=-70
n=5-да является 5 членом
5. найдите сумму десяти первых членов арифм. прогресси (an), если a1=8 a7=24
а7=а1+6д=8+6д=24
6д=16
д=16/6=8/3
а10=8+9*8/3=32
S10=(а1+а10)/2*10=(8+32)/2*10=200