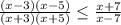
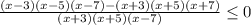
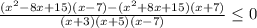
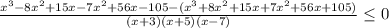
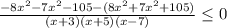
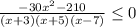
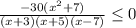
Дверей всего десять. Посмотрим, сколькими можно выбрать две двери.
Пункт А.
Мы не сможем покинуть зал, если обе выбранные двери будут заперты.
Посмотрим, сколькими можно выбрать две запертые двери.
Найдем вероятность того, что обе двери будут заперты.
C24 / C210 = 6/45 = 2/15.
Пункт Б.
Мы сможем покинуть зал, но не сможем войти обратно через другую дверь, если одна из выбранных дверей будет не заперта, а другая – заперта.
Посмотрим, сколькими можно выбрать незапертую дверь.
С
Посмотрим, сколькими можно выбрать запертую дверь:
Найдем вероятность того, что одна дверь будет заперта, а другая – не заперта.
(С16 * C14) / C210 = (6 * 4) / 45 = 8/15.
Пункт В.
Мы сможем покинуть зал и войти обратно через другую дверь, если обе двери будут не заперты.
Посмотрим, сколькими можно выбрать две незапертые двери.
Найдем вероятность того, что обе двери будут не заперты.
C26 / C210 = 15/45 = 1/3.
Пункт Г.
Мы сможем покинуть зал, если произойдет одно из следующих событий:
событие D – одна из дверей будет не заперта, а другая будет заперта;
событие J – обе двери будут не заперты.
Мы уже знаем вероятности этих событий:
P(D) = 8/15 (см. пункт Б);
P(J) = 1/3 (см. пункт В).
А нас интересует сумма этих событий.
P(D + J) = 8/15 + 1/3 = 13/15.
а) 2/15;
б) 8/15;
в) 1/3;
г) 13/15.
числитель ни при каких х не равен нулю
значит отмечаем точки, где выражение не имеет смысла
+ - + -
--------- -5 ------- -3 ----------- 7 -----------------
Значит промежутки решения (-5;-3)∪(7;+∞)
Наименьшее целое решение х= -4