Математика: 2+ x 3x - 4 решите неравенство

Пошаговое объяснение:Правая часть уравнения принимает значения или в зависимости от значений : при при для любого целого В итоге получается уравнение вида которое равносильно уравнениюРассмотрим три промежутка:1) Несложно установить, что только при корни такого вида при заданном диапазоне попадают в промежуток Значит если на этом промежутке уравнение имеет корень, он равен при 2) Аналогично, только при корни такого вида при заданном диапазоне попадают в промежуток Значит если на этом промежутке...

2+ x < 3x - 4 решите неравенство

👇

Увидеть ответ

Ответ:

tashbaeva201

16.11.2020

Раскрываем скобки
x+1+2x+2+3x-3<4x+3x-6
6x<7x-6
ответ x>6

4,7(51 оценок)

Ответ:

kiradark15

16.11.2020

2+х < 3x - 4
2х=8
х=4

2+4 < 3*4-4
6 < 8

4,6(67 оценок)

Открыть все ответы

Ответ:

nastamalysheva

16.11.2020

Пошаговое объяснение:

Число кратне 3 це таке число, яке ділиться націло на 3.

Число ділиться націло на три, якщо сума його цифр ділиться на 3

1) 47 8*1

4+7+8+1=20 - до цього числа потрібно додати замість зірочки таке, щоб утворилося число, яке буде ділитися на три.

20+1=21 : на 3, маємо: 47811

20+4=24 : на з, маємо 47841

20+8=28 : на 3, маємо 47881

2) 6*5 782

6+5+7+8+2=28=2+8=10 - до цього числа потрібно додати замість зірочки таке, щоб утворилося число, яке буде ділитися на три.

10+2 =12 : на 3, маємо: 625 782

10+5=15 : на 3, маємо 655 782

10+8=18 : на 3, маємо 685 782

3) 50*2

5+0+2=7 - до цього числа потрібно додати замість зірочки таке, щоб утворилося число, яке буде ділитися на три.

7+2 = 9 : на 3, маємо 5022

7+5 =12 : на 3, маємо 5052

7+8=15 : на 3, маємо 5082

4,4(89 оценок)

Ответ:

zzizziz

16.11.2020

$a \in \left[ {\frac{\pi }{2};\,\,\frac{{3\pi }}{2} - 3} \right] \cup \left[ {\frac{{5\pi }}{2} - 6;\,\,\frac{{7\pi }}{2} - 9} \right]$

Пошаговое объяснение:

Правая часть уравнения принимает значения 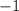или в зависимости от значений :

при $2k - 1 \le x < 2k \cos (\pi \cdot [x]) = - 1,$

при $2k \le x < 2k + 1 \cos (\pi \cdot [x]) = 1$ для любого целого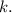

В итоге получается уравнение вида ${\sin ^5}(3x + a) = \pm 1,$ которое равносильно уравнению

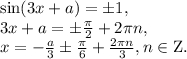
$\sin (3x + a) = \pm 1, \\3x + a = \pm \frac{\pi }{2} + 2\pi n, \\x = - \frac{a}{3} \pm \frac{\pi }{6} + \frac{{2\pi n}}{3}, n \in {\rm{Z}}.$

Рассмотрим три промежутка:

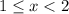
1) $1 \le x < 2$

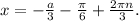
$x = - \frac{a}{3} - \frac{\pi }{6} + \frac{{2\pi n}}{3}.$

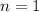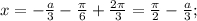
Несложно установить, что только при n = 1 корни такого вида при заданном диапазоне попадают в промежуток $1 \le x < 2.$ Значит если на этом промежутке уравнение имеет корень, он равен $x = - \frac{a}{3} - \frac{\pi }{6} + \frac{{2\pi }}{3} = \frac{\pi }{2} - \frac{a}{3};$

$1 \le \frac{\pi }{2} - \frac{a}{3} < 2$ при $a \in \left[ {0;\,\,\frac{{3\pi }}{2} - 3} \right].$

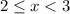
2) $2 \le x < 3$

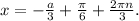
$x = - \frac{a}{3} + \frac{\pi }{6} + \frac{{2\pi n}}{3}.$

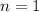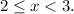Аналогично, только при n = 1 корни такого вида при заданном диапазоне попадают в промежуток $2 \le x < 3.$ Значит если на этом промежутке уравнение имеет корень, он равен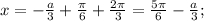 $x = - \frac{a}{3} + \frac{\pi }{6} + \frac{{2\pi }}{3} = \frac{{5\pi }}{6} - \frac{a}{3};$

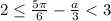$2 \le \frac{{5\pi }}{6} - \frac{a}{3} < 3$ при $a \in \left[ {0;\,\,\frac{{5\pi }}{2} - 6} \right].$

3) $3 \le x \le \pi$

$x = - \frac{a}{3} - \frac{\pi }{6} + \frac{{2\pi n}}{3}.$

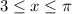
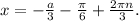
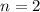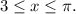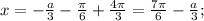
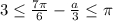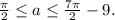
Аналогично, при n = 2 корни такого вида при заданном диапазоне попадают в промежуток $3 \le x \le \pi .$ Значит если на этом промежутке уравнение имеет корень, он равен $x = - \frac{a}{3} - \frac{\pi }{6} + \frac{{4\pi }}{3} = \frac{{7\pi }}{6} - \frac{a}{3};$ $3 \le \frac{{7\pi }}{6} - \frac{a}{3} \le \pi$ при $\frac{\pi }{2} \le a \le \frac{{7\pi }}{2} - 9.$

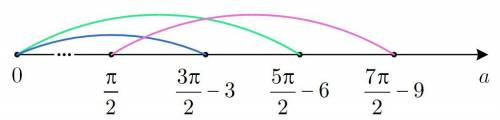
Обозначим на рисунке указанные интервалы. Для существования нечетного количества корней выберем промежутки, на которых пересекаются все три из них или находится только один. Получаем $a \in \left[ {\frac{\pi }{2};\,\,\frac{{3\pi }}{2} - 3} \right] \cup \left[ {\frac{{5\pi }}{2} - 6;\,\,\frac{{7\pi }}{2} - 9} \right]$ .