Пошаговое объяснение:
сначала упростим общий вид членов ряда
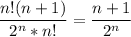
(это можно сделать, пользуясь свойствами пределов - получим равнозначный ряд)
теперь применим ризнак Даламбера
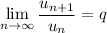
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - неопределенность (дополнительные исследования)
у нас
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас
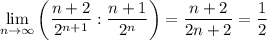
q < 1 - ряд сходится
( можно было и сразу "в лоб" применять признак Даламбера не упрощая формулу - результат был бы тот же...)
Пошаговое объяснение:
сначала упростим общий вид членов ряда
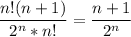
(это можно сделать, пользуясь свойствами пределов - получим равнозначный ряд)
теперь применим ризнак Даламбера
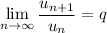
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - неопределенность (дополнительные исследования)
у нас
при q < 1 - ряд сходится, q > 1 - ряд расходится, q = 1 - получаем неопределенность (дополнительные исследования)
у нас
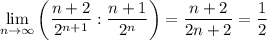
q < 1 - ряд сходится
( можно было и сразу "в лоб" применять признак Даламбера не упрощая формулу - результат был бы тот же...)
3)76-54=22стр на столько стр. меньше осталось прочитать,чем прочитал.
4)54:6=9 дней он прочитает остаток книги