Решение задач :
Задача № 1 :
Преобразуем уравнение к следующему виду: (х – 2006)(у - 2006) = 20062.
Уравнение имеет решения, например, х = у = 4012.
Задача № 2 :
Преобразуем выражение в левой части равенства, учитывая, что α + β + γ = π,
и применяя формулы: cos2x = (1 + cos2x)/2, cosx = - cos(π - x), cosx + cosy = (2cos((x + y)/2))cos((x - y)/2),
получим справедливое тождество. Задача № 4 :
Пусть y = x2 – 3x3. Тогда y' = 2x – 9x2 и с метода интервалов получаем, что y' < 0 при всех x>2/9.
Но 1/4>2/9, следовательно, функция y(x) убывает на луче [1/4; +∞].
Это значит, что x2 - 3x3 < 1/16 - 3/64 = 1/64 < 1/64.
Задача № 5 :
Окружим каждый квадрат полоской шириной 1/2.
Образующие фигуры тоже квадраты со стороной 1 + 2 x 1/2 = 2, имеют площадь равную 4.
Их общая площадь равна 4 x 120 = 480, в то время как искомая площадь равна 500.
Следовательно, найдется точка, которая не покрыта построенными квадратами, но это значит, что она удалена от данных квадратов не меньше чем на по всем направлениям.
Круг радиуса с центром в этой точке не имеет общих точек ни с одним из квадратов.
ответ: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Пусть пуд сахара стоит х, а фунт чая - y. Тогда можем составить и решить такую систему уравнений:
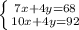
Решаем систему методом вычитания (находим x):
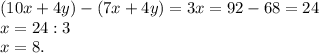
Теперь можно найти y:
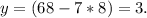
Итого: пуд сахара стоит 8 рублей, а фунт чая - 3 рубля.
Задачу можно решить и арифметически, заметив, что и там, и там по 4 фунта чаю:
1). 92 - 68 = 24 (рубля) - разница между 7 пулами и 10 пудами сахара.
2). 10 - 7 = 3 (пуда) - разница между 7 пудами и 10 пудами сахара.
3). 24 : 3 = 8 (рублей) - стоит пуд сахара.
4). (68 - 8 * 7) : 4 = 3 (рубля) - стоит фунт сахара.
90
Пошаговое объяснение:
Если девочки составляют 3/5 от общего числа детей, то число мальчиков составляет 1 - 3/5 = 2/5 от того же числа. Это означает, что общее число детей равно 60:2/5 = 150, и девочек в этом лагере 150 - 60 = 90.