Условия определения логарифмической функции:
1) - логарифмируемое выражение должно быть положительным,
2) - знаменатель дроби не должен быть равен 0.
1) Чтобы логарифмируемое выражение было положительным, надо, чтобы числитель и знаменатель были одновременно или положительными или отрицательными:
2х + 1 >0 x > -1/2
x - 1 > 0 x > 1 Первое решение х > 1
2х + 1 <0 x < -1/2
x - 1< 0 x < 1 Второе решение х < - 1/2
2) Чтобы знаменатель дроби не был равен 0: х - 1 ≠ 0 х ≠ 1.
ответ: -1/2 > x > 1 . надеюсь если не правильно не бань меня
1) Начнём с угла 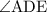 . Поскольку даны квадрат и правильный треугольник, то этот угол равен сумме углов квадрата и правильного треугольника, т.е.
. Поскольку даны квадрат и правильный треугольник, то этот угол равен сумме углов квадрата и правильного треугольника, т.е. 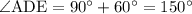
2) Теперь, т.к. треугольник 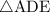 - равнобедренный (по построению
- равнобедренный (по построению 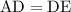 ), то углы при его основании равны. Поскольку сумма углов в треугольнике равна
), то углы при его основании равны. Поскольку сумма углов в треугольнике равна 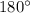 , то получим
, то получим 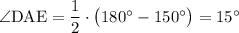
3) 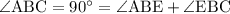 , но из равенства треугольников по трём сторонам (
, но из равенства треугольников по трём сторонам (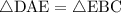 ) получим
) получим 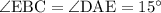 . Следовательно,
. Следовательно, 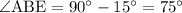
4) 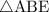 - равнобедренный. Отсюда,
- равнобедренный. Отсюда, 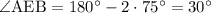
5) Т.к.  , а
, а 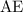 и
и 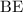 - секущие, причём такие, что
- секущие, причём такие, что  - равнобедренный, то
- равнобедренный, то 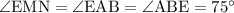
ответ. 1) 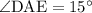 ; 2)
; 2) 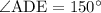 ; 3)
; 3)  ; 4)
; 4) 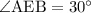 ; 5)
; 5)