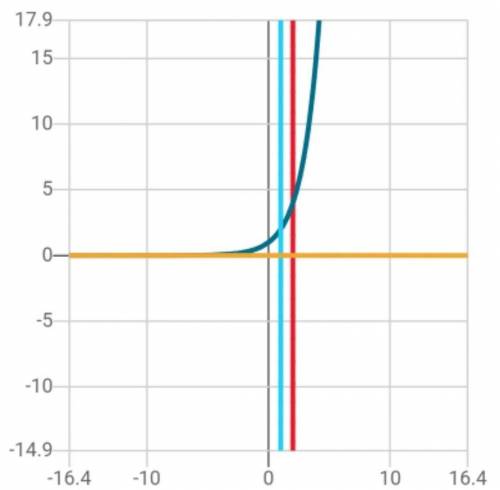
Построим графики функции на одной координатной плоскости (см. приложение).
Увидим кусочек криволинейной трапеции.
Воспользуемся формулой Ньютона-Лейпцина (см. приложение 2)
Получим:
2^x*ln2 |²1
Подставим циферки
2²ln2 - 2¹ln2
Посчитаем, че там у нас получилось
4ln2-2ln2
Благодаря элементарным навыкам в решении математические задач, мы можем польчить следующее
2ln2
И вот чудо, чуть посложнее, конечно, но мы может использовать одну из формул логарифмов
ln4
Не очень красивая площадь вышла, но тем не менее, она равна ln4
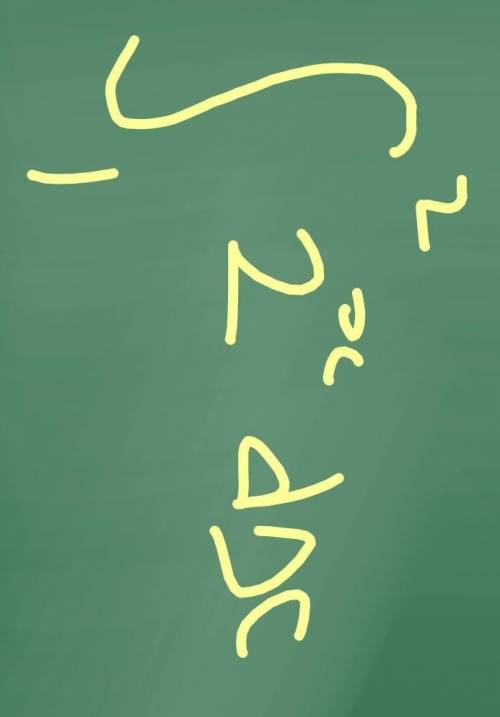
Всего было 49 рыбок.
Пошаговое объяснение:
1) 7+2=9(аквариумов) после допол
нительной установки.
По условию число рыбок менее 80.
Только в одном аквариуме рыбок
на 4 больше, чем в остальных.
2) 9-1=8 аквариумов, в которых ры
бок поровну.
3) Пусть в каждом из 8 аквариумов
по х рыбок, тогда в восьми аквари
умах расселили 8х рыбок.
В девятом аквариуме на 4 рыбки
больше, чем в каждом из осталь
ных, то есть (х+4) рыбок.
Всего рыбок:
8х+(х+4)
Составим неравенство:
8х+(х+4)<80
8х+х+4<80
9х+4<80
9х<80-4
9х<76
х<76/9
Количество рыбок есть число нату
ральное ( x€N ) ==>
x может принимать значения, крат
ные 7 (ведь раньше рыбки жили в
семи аквариумах и в каждом их бы
ло поровну).
Должно выполняться условие:
число (х-4) должно быть кратно 9.
Кроме того:
х<=8
Перебираем возможные варианты.
Подходит число х=5.
Считаем сколько всего было рыбок:
8×5+(5+4)=40+9=49
До установки дополнительных ак
вариумов в каждом было по
49:7=7 ( рыбок).
Когда аквариумов стало девять,
рыбок расселили в 8 аквариумах
поровну по
(49-4):9=5 (штук) в каждом, кроме
одного.
В девятом аквариуме рыбок было
5+4=9 (штук).
Всего было 49 рыбок.