1. Средняя скорость движения - это отношения всего пройденного пути к затраченному времени.
2. Обращаем внимание на условие задачи: автомобиль двигался половину времени (а не половину пути, как обычно бывает в задачах) со скоростью 80 км/ч, а вторую половину времени со скоростью 100 км/ч.
3. Обозначим все затраченное время через T. Тогда за первую половину времени движения автомобиль проехал расстояние L1 = (T / 2) * 80 = 40 *T км.
4. За вторую половину времени движения автомобиль проехал расстояние
L2 = (T / 2) * 100 = 50 * T км.
5. Тогда средняя скорость движения Vср = (L1 + L2) / T = (40 * T + 50 * T) / T = 90 км/ч.
ответ: средняя скорость движения автомобиля 90 :
Имеем дело с однородной СЛАУ, у которой кол-во неизвестных больше кол-ва уравнений, значит, имеем нетривиальные решения.
Приведем матрицу к ступенчатому виду:
![\left[\begin{array}{cccc}-4&1&2&1\\7&4&1&0\\1&2&5&0\end{array}\right]](/tpl/images/1148/9647/1ba93.png)
Меняем 1 и 3 строки:
![\left[\begin{array}{cccc}1&2&5&0\\7&4&1&0\\-4&1&2&1\end{array}\right]](/tpl/images/1148/9647/483ee.png)
Вычитаем из второй строки первую, умноженную на 7:
![\left[\begin{array}{cccc}1&2&5&0\\0&-10&-34&0\\-4&1&2&1\end{array}\right]](/tpl/images/1148/9647/91dae.png)
Делим на -2 вторую строку и прибавляем к 3 строке первую, умноженную на 4:
![\left[\begin{array}{cccc}1&2&5&0\\0&5&17&0\\0&9&22&1\end{array}\right]](/tpl/images/1148/9647/64e50.png)
Вычитаем из 3 строки вторую:
![\left[\begin{array}{cccc}1&2&5&0\\0&5&17&0\\0&4&5&1\end{array}\right]](/tpl/images/1148/9647/7a4f0.png)
Вычитаем из 2 строки третью:
![\left[\begin{array}{cccc}1&2&5&0\\0&1&12&-1\\0&4&5&1\end{array}\right]](/tpl/images/1148/9647/149c0.png)
Вычитаем из 3 строки вторую, умноженную на 4:
![\left[\begin{array}{cccc}1&2&5&0\\0&1&12&-1\\0&0&-43&5\end{array}\right]](/tpl/images/1148/9647/7a475.png)
Ранг равен трем, откуда количество свободных переменных равно 4 - 3 = 1. Пусть D - свободная переменная. Тогда
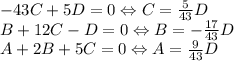
Значит,
![\left[\begin{array}{c}A\\B\\C\\D\end{array}\right] = D\left[\begin{array}{c}\frac{9}{43} \\{-\frac{17}{43}}\\\frac{5}{43}\\1\end{array}\right] = \tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/c00d2.png)
ответ: векторы вида ![\tilde{D}\left[\begin{array}{c}9\\-17\\5\\43\end{array}\right]](/tpl/images/1148/9647/1e9f9.png) , при
, при 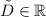 .
.
⇒11/21 > 1/21 ⇒(6/7-1/3)>(1/3-2/7 )
2)1/3-2/7 =7/21-6/21=1/21
3)6/7-2/5 =30/35-14/35=16/35
⇒16/35>4/35 ⇒(6/7-2/5)>(2/5-2/7)
4)2/5-2/7=14/35-10/35=4/35
11/21 =(6/7-1/3) 16/35=(6/7-2/5)
55/105 > 48/105 ⇔(6/7-1/3) -наибольшая