Периметр прямоугольного треугольника равен 60 см. Высота, проведенная к гипотенузе, равна 12 см. Найти площадь треугольника.
* * *
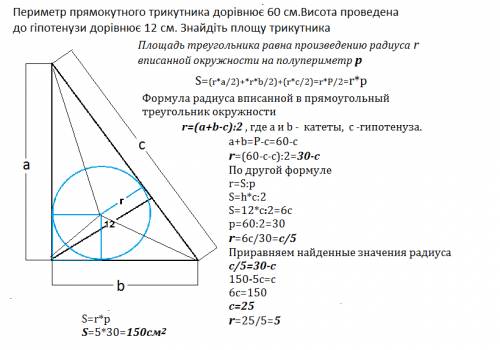
Площадь треугольника равна произведению радиуса r вписанной окружности на полупериметр р
Формула радиуса вписанной в прямоугольный треугольник окружности
r=(a+b-c):2 , где а и b - катеты, c -гипотенуза.
a+b=P-с=60-c
r=(60-c-c):2=30-c
По другой формуле
r=S:p
S=h*c:2
S=12*c:2=6c
р=60:2=30
r=6c/30=c/5
Приравняем найденные значения радиуса
c/5=30-c
150-5c=c
6c=150
c=25 см
r=25/5=5 см
S=r*p=5*30=150 см²
Дальше приравниваем производную к нулю:
Поскольку тут всё предельно просто, не буду прибегать к методу интервалов, а объясню "на пальцах".
Если говорить кратко, то напомню, что, когда производная больше нуля, то функция возрастает,а если меньше нуля, то убывает. Нас, исходя из условия, интересует возрастание.
Т.е. теперь нам нужно решить неравенство вида:
ответ: