Периметр прямоугольника по формуле: Р = 2*(a+b).
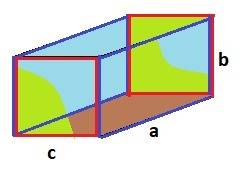
Рисунок к задаче в приложении.
ДАНО: a = 4 м, b = 3 м, c = 3 м.
РЕШЕНИЕ
Из рисунка видно, что можно применить два варианта расчёта.
Вариант 1. Сумма периметров двух пар стен.
Р₁ = 2*(a+b) = 2*(4+3) = 14 м - периметр длинной стены.
Р₂ = 2*(b+c) = 2*(3+3) = 12 м - периметр короткой стены.
Р = 2*(Р₁+Р₂) = 2*(14+12) = 52 м - периметр стен - ОТВЕТ 1
Вариант 2. Сумма длин всех рёбер прямоугольника плюс 4 длины высоты стен.
Формула суммы длин рёбер параллелепипеда:
P₁ = 4*(a+b+c) = 4*(4+3+3) = 4*10 = 40 метров
Р = Р₁ + 4*b = 40 + 4*3 = 40+12 = 52 м - периметр - ОТВЕТ 2
Из центра В второй окружности проведём перпендикуляр ВК к хорде СЕ.
Точка К будет серединой СЕ (по свойству хорды).
Найдём длину отрезка ВК:
ВК = √(ВЕ²-КЕ²) = √(10²-6²) = √(100-36) = √64 = 8.
Имеем четырёхугольник ОСКВ с двумя прямыми углами С и К.
Проведём перпендикуляр из точки О к отрезку ВК.
Получим прямоугольный треугольник с катетами 6 и (8 - r).
Гипотенуза этого треугольника равна радиусу r.
r² = 6² + (8 - r)².
r² = 36 + 64 -16r + r².
16r = 100.
r = 100/16 = 25/4 = 6,25.