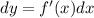 или
или 

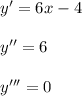


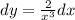
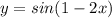




17 см другая сторона прямоугольника
Пошаговое объяснение:
Периметр квадрата со стороною 14 см = периметру прямоугольника, одна из сторон которого = 11 см
Найти вторую сторону прямоугольника.
Р квадрата = 4а, где а - сторона квадрата = 14 см
Р квадрата = 4*14 = 56 см
Р прямоугольника = 2(а+b), где Р = 56 см, а - одна сторона прямоугольника = 11 см, b - другая сторона прямоугольника = ?см
Р прямоугольника = 2(а+b)
56 = 2(11+b)
56/2 = 11+b
28 = 11+b
b = 28 - 11
b = 17 см другая сторона прямоугольника
Р прямоуг. = 2(11+17) = 2*38 = 56 (см)
1. Область определения функции: x ∈ (-∞; ∞).
2. Точки пересечения с осью координат X.
График функции пересекает ось X при f = 0, значит надо решить уравнение: x³ - 3x = 0.
x(x² - 3) = 0. Получаем 3 корня
x₁ = 0, х₂ = √3, х₃ = -√3.
3. Точки пересечения с осью координат Y.
График пересекает ось Y, когда x равняется 0:
подставляем x = 0 в x³ - 3x.
0³ - 3*0 = 0.
Результат:
f(0) = 0.
Точка:
(0, 0).
4. Экстремумы функции.
Для того, чтобы найти экстремумы, нужно решить уравнение
d
--(f(x)) = 0
dx
(производная равна нулю), и корни этого уравнения будут экстремумами данной функции:
d
--(f(x)) = 3x² - 3.
dx
3x² - 3 = 0
Решаем это уравнение: 3(х² - 1) = 0,
Корни этого уравнения x₁ = 1 и х₂ = -1.
Значит, экстремумы в точках:
(-1, 2)
(1, -2)
5. Интервалы возрастания и убывания функции:
Найдём интервалы, где функция возрастает и убывает, а также минимумы и максимумы функции, для этого смотрим как ведёт себя функция в экстремумах при малейшем отклонении от экстремума:
х = -2 -1 0 1 2y' = 9 0 -3 0 9
Минимумы функции в точках: x_{2} = 1.
Максимумы функции в точках: x_{2} = -1.
Убывает на промежутках (-oo, -1] U [1, oo)
Возрастает на промежутках [-1, 1]
6. Точки перегибов
Найдем точки перегибов, для этого надо решить уравнение
2
d
---(f(x)) = 0
2
dx
(вторая производная равняется нулю), корни полученного уравнения будут точками перегибов для указанного графика функции,
2
d
---(f(x)) =
2
dx
6х = 0.
Решаем это уравнение.
Корни этого уравнения x1 = 0.
7. Интервалы выпуклости и вогнутости:Найдём интервалы, где функция выпуклая или вогнутая, для этого посмотрим, как ведет себя функция в точках перегибов:
Вогнутая на промежутках [0, oo)
Выпуклая на промежутках (-oo, 0]
8. Горизонтальные асимптоты
Горизонтальные асимптоты найдём с пределов данной функции при x->+oo и x->-oo
\lim_{x \to -\infty}\left(x^{3} - 3 x\right) = -∞.
Значит, горизонтальной асимптоты слева не существует
\lim_{x \to \infty}\left(x^{3} - 3 x\right) = ∞.
Значит, горизонтальной асимптоты справа не существует.
9. Наклонные асимптоты
Наклонную асимптоту можно найти, подсчитав предел функции x^3 - 3*x, делённой на x при x->+oo и x ->-oo
\lim_{x \to -\infty}\left(\frac{1}{x} \left(x^{3} - 3 x\right)\right) = ∞
Значит, наклонной асимптоты слева не существует.
\lim_{x \to \infty}\left(\frac{1}{x} \left(x^{3} - 3 x\right)\right) = ∞.
Значит, наклонной асимптоты справа не существует.
10. Чётность и нечётность функции
Проверим функци чётна или нечётна с соотношений f = f(-x) и f = -f(-x).
Итак, проверяем:
x^{3} - 3 x = - x^{3} + 3 x.
- Нет
x^{3} - 3 x = - -1 x^{3} - 3 x.
- Нет.
Значит, функция не является ни чётной, ни нечётной.
11. График дан в приложении.