DD1 = R /2.
Отсюда O1D = 2 R /3 − R /2 = R /6 . Так как АD = ½ AC = R √3 /2, то
ответ. R √7/3
1.2. B треугольнике AOB (рис. P.1.2) известны: ∠ BAO = α/2 , ∠ AOB = α/2 + π/2, BO = m· По теореме синусов находим AB = m ctg α/2· Теперь можно найти AC и R = ВО1:
AC = 2AD = 2АВ sin (π/2 − α) = 2АВ cos α = 2m ctg α/2 cos α,
ответ.
1.3. Условие задачи может быть геометрически осуществлено в двух случаях (рис. Р.1.3, а), т. е. когда треугольник либо правильный, либо равнобедренный тупоугольный (докажите). Решить эту задачу можно сразу для обоих случаев. На рис. Р.1.3, б изображены треугольник ABC и треугольник А1В1С1, составленные из средних линий первого треугольника. Треугольник А1В1С1 подобен треугольнику ABC с коэффициентом подобия половина. Следовательно, радиусы окружностей, описанных около этих треугольников, относятся как один к двум.
1.4. Если сторона а треугольника ABC биссектрисой АА1 разделена на отрезки а1 и а2, то можно записать следующие соотношения (рис Р. 1.4.):
Решая эту систему уравнений относительно a1 и а2, получим
Вычислим аналогично отрезки, на которые разделены стороны b и с треугольника ABC:
Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, то
Аналогично находим
Теперь найдем отношение
ответ.
1.5. Выразим площадь треугольника ABC через радиус r вписанной окружности и углы А, B и С треугольника.
9 попыток
Пошаговое объяснение:
АБСД - 4х значный пароль
А может быть или 0 или 1 или 2 - три варианта
Б может быть или 1 или 2 или 0 - три варианта
С может быть или 1 или 2 или 0 - три варианта
Д может быть или 1 или 2 или 0 - три варианта
3*3*3*3=81 - количество 4-хзначных чисел, которые можно составить из чисел 1,2,0
Например: 0000, 0222, 1200
Известно, что каждая попытка позволяет проверить правильность не только самого номера, но и всех номеров, отличающихся от введённого ровно в одной позиции
0000--0001--0002--0010--0020--0100--0200--1000--2000
0222--0220--0221--0202--0212--0022--0122--1222--2222
1200--1201--1202--1210--1220--1000--1100--0200--2200
Вывод 1: из каждого номера можно получить 8 номеров, отличающихся от начального ровно в одной позиции
Значит одним номером (паролем), Эдик может проверить 9 номеров
Вывод 2:
81 : 9 = 9 - номеров должен ввести Эдик, что бы проверить все 81 пароли
Определим один вариант паролей, которые может ввести Эдик (9штук)
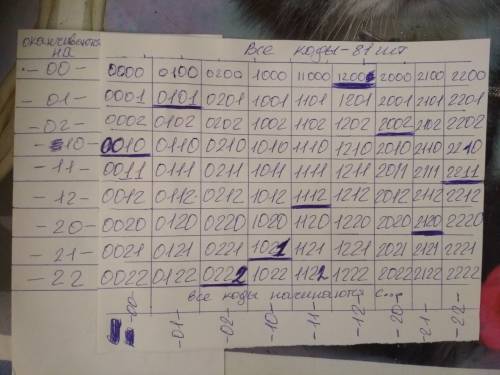
1) напишем все варианты паролей - 81 номеров
2) сгруппируем все номера по двум последним числам (-00-,-01-,-02-,-10-,-11-,-12-,-20-,-21-,-22-) получилось 9 групп
3) в каждой группе, разместим номера в порядке возрастания
-------- смотрите фото --------
4) из полученной таблице выберите числа
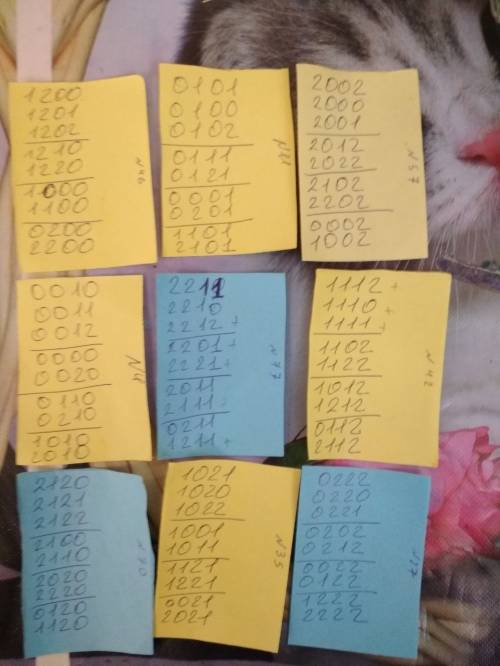
5) проверим выбранные номера и номера отличающиеся от них в одной позиции на "повторки" (повторов быть не должно)
У нас получились номера (смотрите фото)
1200--0101--2002--0010--2211--1112--2120--1021--0222
Если прописать эти числа и числа, отличающихся от них в одной позиции, получится 81 пароль (повторов нет). Смотри фото)))
Как видно из таблицы (фото), мы взяли по одному числу из каждой группы (строки) и каждого столбца
Вывод: с таблицы можно найти все 9 вариантов паролей (по 9 штук в каждой). И в каждом варианте одно число будет оканчиваться на -00-, второе на -01-, третье на -02-, четвертое на -10-, пятое -11-, шестое на -12-, седьмое на -20-, восьмое на -21-, девятое на -22-.
ответ: 9 попыток