Р = 28 см,
d = 10 см,
1.
полупериметр р:
р = 1/2 * Р,
р = 1/2 * 28 = 14 см,
2.
р = а + в, значит
а + в = 14 см,
3.
пусть
длина а = х,
ширина в = (14 - х),
4.
две соседние стороны и диагональ образуют прямоугольный треугольник, поэтому по теореме Пифагора:
d² = а² + в²,
получаем уравнение:
10² = х² + (14 - х)²,
100 = х² + 196 - 28х + х²,
2х² - 28х + 96 = 0,
х² - 14х + 48 = 0,
Д = 196 - 192 = 4,
х1 = (14+2)/2 = 8 см - длина,
х2 = (14-2)/2 = 6 см,
14-х1 = 14-8 = 6 см - ширина,
14-х2 = 14-6 = 8 см,
ответ: стороны прямоугольника равны 6 и 8 см
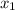 = 2 ;
= 2 ; 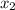 = 7
= 7
Пошаговое объяснение:
1. Переместим выражение в левую часть и изменим его знак
x²-7x+23=2x+9 = x²-7x+23-2x-9=0
2. Приведём подобные члены
x²-7x+23-2x-9=0 = x²-9x+23-9=0
3. Вычитаем числа
x²-9x+23-9=0 = x²-9x+14=0
4. Запишим -9x в виде разности
x²-9x+14=0 = x²-2x-7x+14=0
5. Вынесем за скобки общий множитель x
x²-2x-7x+14=0 = x(x-2)-7x+14=0
6. Вынесем за скобки общий множитель -7
x²-2x-7x+14=0 = x(x-2)-7(x+2)=0
7. Вынесем за скобки общий множитель x-2
x(x-2)-7(x+2)=0 = (x-2)(x-7)=0
8. Если произведение равняется 0, то как минимум один из множителей должен быть равен 0
x-2=0
x-7=0
9. Решим уравнение относительно x
x=0
x=7
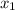 = 2 ;
= 2 ; 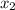 = 7
= 7
3+2=5(таня)
2+5+3=10(всего)