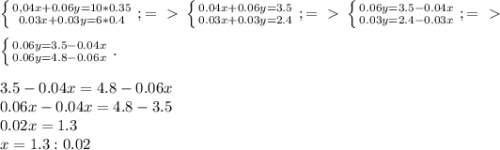
2 раза
Пошаговое объяснение:
Разделы теорииКликните, чтобы открыть меню Главная > Классическое определение вероятности Классическое определение вероятности 1. Читай полную теорию 2. Вникай в доказательства 3. Применяй на практике Факт 1. Случайное событие – это событие, которое при данных условиях может произойти, а может не произойти. Например, событие “при бросании игральной кости выпало 3 или 4 очка”. Напомним, что игральная кость – это кубик с шестью гранями, на которых написаны числа от 1 до 6. Предположим, что мы проводим некоторое испытание (эксперимент), например, бросаем игральную кость. Результатом нашего испытания может быть одно из шести событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков. Такие события называются элементарными событиями (то есть это “простейшие” события, которые в совокупности образуют все множество исходов нашего эксперимента). Например, событие “при бросании игральной кости выпало 3 или 4 очка” не является элементарным, оно состоит из двух элементарных событий “при бросании игральной кости выпало 3 очка” и “при бросании игральной кости выпало 4 очка”. Если сложить вероятности всех возможных элементарных событий у некоторого эксперимента, то получится 1. Два события мы будем называть равновероятными (равновозможными), если вероятности наступления любого из них одинаковы. Например, при бросании игральной кости вероятности любого из событий: выпадет 1 очко, выпадет 2 очка, 3 очка, 4 очка, 5 очков или 6 очков, одинаковы. Или, например, при подбрасывании монеты вероятности событий “выпадет орел” и “выпадет решка” также одинаковы. Примером неравновероятных событий могут послужить два события: “при бросании игральной кости выпадет 1 очко” и “при бросании игральной кости выпадет нечетное количество очков”. Почему? В первом случае нам удовлетворяет только исход, когда кубик упадет кверху гранью, на которой написано 1; во втором случае нам подходит целых три исхода: он может выпасть кверху гранью.
7х+1-9х-3=5
-2х-2=5
-2х=5+2
-2х=7
Х=7:(-2)
Х= -7/2= -3 1/2= -3,5
Проверка
(7• -3,5+ 1)- (9•(-3,5)+ 3)= 5
(-24,5+ 1)- (-31,5+ 3)= 5
-23,5-(-28,5)= 5
-23,5+28,5=5
5=5
3.4+2y=7(y-2.3)
3,4+ 2у= 7у-7•2,3
3,4+2у= 7у- 16,1
3,4+16,1=7у-2у
19,5= 5у
У= 19,5: 5
У= 3,9
Проверка
3,4+ 2•3,9= 7•(3,9-2,3)
3,4+7,8=7•1,6
11,2=11,2
0.2(7-2y)=2.3-0.3(y-6)
0,2•7- 0,2•2у= 2,3- 0,3•у+ 0,3•6
1,4- 0,4у= 2,3- 0,3у+ 1,8
-0,4у+0,3у= 2,3+1,8-1,4
-0,1у= 2,7
У=2,7:(-0,1)
У= -27
Проверка
0,2•(7-2•(-27))= 2,3-0,3•((-27)-6)
0,2•(7+54)= 2,3-0,3•(-33)
0,2•61= 2,3+9,9
12,2= 12,2
2/3(1\3x-1\2)=4x+две целых одна вторая
2/3• (1/3х-1/2)= 4х+ 2 1/2
2/3• 1/3х- 2/3• 1/2= 4х+ (2•2+1)/2
(Сократили 2/3 и 1/2 (2 и 2 на 2))
2/9х- 1/3•1/1= 4х+ 5/2
2/9х- 1/3= 4х+5/2
-1/3-5/2= 4х- 2/9х
-(1/3+5/2)= 3 9/9х -2/9х
-( (1•2)/(3•2) + (5•3)/(2•3) )= 3 7/9х
-(2/6+ 15/6)= (3•9+7)/9х
-17/6= 34/9х
Х= (-17/6): 34/9
Х= (-17/6)• 9/34
Х= (-1/2)• 3/2
(Сократили 17 и 34 на 17; 9 и 6 на 3)
Х= -3/4= -0,75
Проверка
2/3•(1/3х-1/2)= 4х+ 2 1/2
2/3• (1/3• -3/4 - 1/2)= 4 • -3/4+ 2 1/2
2/3• (1/1• -1/4 -1/2)= 1• -3/1+ 2,5
2/3• (-(1/4+ 1/2))= -3+ 2,5
2/3• -( 1/4+ (1•2)/(2•2))= -0,5
2/3• (- (1/4+2/4)= -0,5
2/3• (-3/4)= -0,5
1/1• (-1/2)= -0,5
-1/2= -0,5
-0,5= -0,5