(см. объяснение)
Пошаговое объяснение:
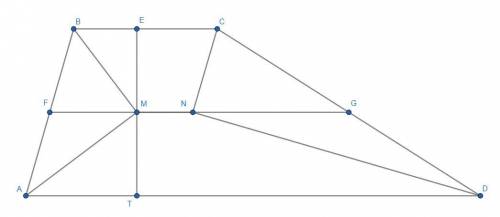
Покажем сначала, что биссектрисы AM и BM пересекаются под прямым углом. Действительно, пусть ∠ABC=α и ∠BAD=β. Тогда α+β=180°. Так как биссектриса делит угол пополам, то верно, что ∠ABM+∠BAM=α/2+β/2=90°, поэтому и ∠BMA=90°.
Опустим из точки M перпендикуляр на сторону BC. Получим ME⊥BC. Тогда ΔBMA~ΔBEM по двум углам. Из подобия треугольников следует, что AB/BM=AM/ME.
Опустим из точки M перпендикуляр на сторону AD. Получим, MT⊥AD. Тогда ΔBMA~ΔATM по двум углам. Из подобия треугольников следует, что AB/AM=BM/MT, то есть AB/BM=AM/MT.
Так как AB/BM=AM/ME и AB/BM=AM/MT, то верно, что AM/ME=AM/MT или ME=MT.
Так как расстояния от точки M до прямых BC и AD одинаковы, то точка M лежит на средней линии трапеции.
Применив аналогичное рассуждение, получаем, что точка N тоже лежит на средней линии трапеции.
Тогда MN - это часть средней линии трапеции, то есть MN||BC и MN||AD.
Проведем среднюю линию трапеции FG. По определению FG=(7+12)/2=19/2.
Так как треугольники ΔBMA и ΔCND прямоугольные, а F и G - середины их гипотенуз AB и CD, то FM и GN - это медианы, равные AB/2 и CD/2 соответственно, то есть FM=5/2 и GN=4.
Понятно, что MN=FG-FM-GN, а значит MN=19/2-5/2-4=3.
Задача решена!
45 человек
Пошаговое объяснение:
если 90 говорят по-испански, то 10 НЕ говорят по-испански (100-90), т.е они НЕ говорят на трех языках
так же 20 НЕ говорят по-итальянски (100-20), т.е НЕ говорят на трех языках
25 Не говорят по-китайски (100-75), т.е. не говорят на трех языках
учитывая допущение "по меньшей мере" мы можем допустить, что все эти люди - разные люди и тогда на трех языках НЕ говорят
10+20+25 = 55 человек и тогда оставшиеся люди - 45 человек - (опять же "по меньшей мере") могут говорить на трех языках...
a=1,6 дм = 16 см
b=25 см
S-?
S=a×b=16×25=400 см^2 немесе 40 дм^2