По свойству медианы в равнобедренном треугольнике:
Медиана в прямоугольном треугольнике, проведённая из прямого угла к гипотенузе равна её половине.
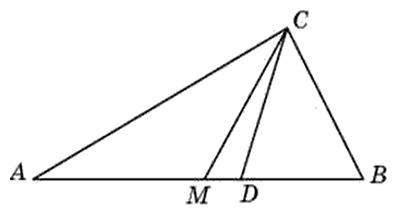
1) Рассмотрим ΔACM - он равнобедренный где AM=MC
а значит ∠CAM=∠ACM
Из ΔACD где CD= биссектриса ΔABC можно найти ∠ACM
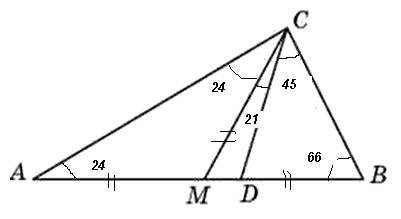
∠ACM=∠АCD-∠MCD=45°-21°=24°
т.к. ∠CAM=∠ACM=24°
Сумма углов ΔABC=180°. значит ∠CBA=180°-24°-90°=66°
Меньший угол = 24°
2) Можно рассмотреть и другой случай:
Рассмотрим ΔMCB
он равнобедренный где MC=MB
отсюда ∠MCB=∠CBM
∠MCB=45°+21°=66°=∠CBM
А значит ∠CAB=180°-90°-66°=24°
0,3х= -4,2-0,9
0,3х= -5,1
х= -5,1÷0,3
х= -17
2) (2-х)(х+3)=0
2-х=0
▪х1=2
х+3=0
х2= -3
ответ: (х1; х2)=(2; -3)