a(a + 5b) - (a + b)(a - b)=a^2+5ab-a^2+b^2=5ab+b^2
b(3a-b) - (a - b)(a + b)=3ab-b^2-a^2+b^2=3ab-a^2
(y+10)(y-2)-4y(2 - 3y)=y^2+8y-20-8y+12y^2=13y^2-20
(a-4)(a+9)-5a(1-2a)=a^2+5a-36-5a+10a^2=11a^2-36
(2b-3)(3b+2)-3b(2b+3)=6b^2-9b+4b-6-6b^2-9b=-14b-6
(3a-1)(2a-3)-2a(3a+5)=6a^2-2a-6a+4-6a^2-10a=-18a+4
(m+3)^2 -(m-2)(m+2)=m^2+6m+9-m^2+4=5m+13
(a-1)^ - (a+1)(a-2)=a^2-2a+1-a^2-a-2=-3a-1
(c+2)(c--1)^2=c^2-c-6-c^2+2c-1=c-7
(y-4)(y+-3)^=y^2-16-y^2+6y-9=6y-25
(a-2)(a++1)^ =a^2+2a-8-a^2-2a-1=-9
(b-4)(b+-1)^=b^2-2b-8-b^2+2b-1=-9
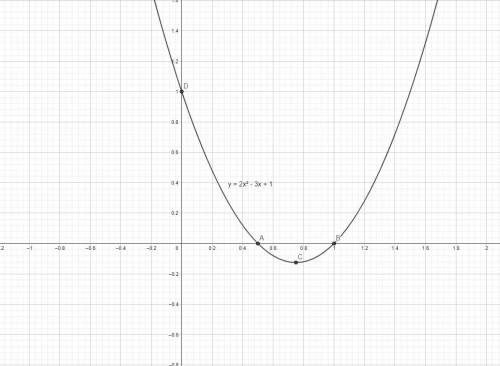
График построен.
Пошаговое объяснение:
y = 2x² - 3x + 1 - парабола, ветви которой направлены вверх (так как a > 0).
Найдём точки пересечения графика с осью ОХ. Для этого найдём корни уравнения:
2x² - 3x + 1 = 0
По т-ме Виета корни: x₁ = 1; x₂ = c/a = 0,5.
Получаем: y = 2(x - 1)(x - 0,5)
График пересекает ось ОХ в двух точках: 1 и 0,5.
Найдём вершину:
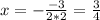
y = 2 * 0,75² - 3 * 0,75 + 1 = -0,125
Итак, вершина: (0,75; -0.125). Строим график (фото).
На фото:
т.С (0,75; - 0,125) - вершина;
т.А (0,5; 0) - первая точка пересечения графика с осью ОХ;
т.В (1; 0) - вторая точка пересечения графика с осью ОХ.
т.D (0; 1) - точка пересечения графика с осью OY.