События: x1 - обратился с иском первый, x2 - обратился с иском второй, x3 - обратился с иском третий, x - не x.
p(x1)= 0.24, p(x2) = 0.29, p(x3) = 0.19
Итак, вероятность того, что в страховую компанию обратится хотя бы один клиент с иском, равна сумме вероятностей, что в компанию обратится первый и не обратятся двое других, обратится второй и не обратятся двое других, обратится третий и не обратятся двое других, обратятся первый и второй, но не третий, первый и третий, но не второй, второй и третий, но не первый, и обратятся все три.
Вероятности этих событий мы складываем, так как они попарно несовместны, а по следствию из теоремы о сложении вероятности несовместных событий: вероятность того, что произойдёт одного из нескольких попарно несовместных событий, равна сумме вероятностей этих событий.
p = p(x1x2x3)+p(x1x2x3)+p(x1x2x3)+p(x1x2x3)+p(x1x2x3)+p(x1x2x3)+p(x1x2x3).
Воспользовавшись тем фактом, что события x1x2x3, x1x2x3, x1x2x3, x1x2x3, x1x2x3, x1x2x3, x1x2x3, x1x2x3 - образуют полную группу событий, а значит сумма вероятностей этих событий будет равна 1, будем считать: p = 1 - p(x1x2x3)
p(x1) = 1 - 0.24 = 0.76, p(x2) = 1 - 0.29 = 0.71, p(x3) = 1 - 0.19 = 0.81
События x1, x2, x3 - независимы. По следствию из теоремы об умножении вероятностей: вероятность совместного их наступления равна произведению вероятностей наступления каждого из них.
p = 1 - p(x1x2x3) = 1 - p(x1)p(x2)p(x3) = 1 - 0.76*0.71*0.81 = 1 - 0.437076 = 0.562924
D(X)=50/81
Закон распределения на первой картинке
Пошаговое объяснение:
начнем с того, что хотя бы один букет из роз был продан, так как было продано 5 букетов, а НЕ из роз всего 4.
Значит Х - число проданных букетов, составленных из роз, может быть от 1 до 5
1) Если продан 1 букет роз, то его можно выбрать из 5 возможных , а оставшиеся 4 букета продали НЕ из роз, из 4 возможных.
Значит все возможные ищутся через сочетания (благоприятный исход)
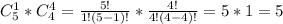
Число всех исходов: проданы 5 букетов из 9 возможных:
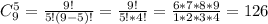
Тогда по классическому определению вероятности:
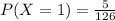
Аналогично с остальными
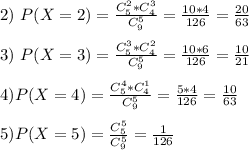
Обязательно проверяем, чтобы сумма полученных вероятностей равнялась 1
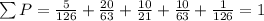
Проверка выполняется, значит вероятности найдены верно!
Данное распределение называется гипергеометрическое
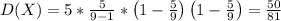


Vc = 30 км/ч
Vт = 4 1/2 км/ч
S по теч. = 23 км
S пр.теч. = 17 км
1) Время на путь по течению реки:
t по теч. = S по теч. ÷ (Vc +Vт)
t по теч. = 23 ÷ (30 + 4 1/2 ) = 23 ÷ 34 1/2 = = 17÷ (69/2) =
= 17 * (2/69) = (17*2)/69 = (1*2)/3 = 2/3 (часа)
2) Время на путь против течения:
t против теч. = S пр. теч. ÷ (Vc -Vт)
t пр. теч. = 17 ÷ ( 30 - 4 1/2) = 17÷ 25 1/2 = (17*2)/(1*51)= 2/3 (часа)
ответ: за 2/3 часа теплоход преодолеет 23 км по течению реки
или 17 км против течения реки.