7/Задание № 7:
На двух параллельных прямых отметили семь точек: три на одной и четыре на другой. Сколько существует четырёхугольников с вершинами в этих точках?
РЕШЕНИЕ: Понятно, что две точки нужно выбрать с одной прямой, а две - с другой, иначе три точки будут лежать на одной прямой и в качестве фигуры получится треугольник.
Выбрать две точки с первой прямой: 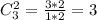
Выбрать две точки со второй прямой: 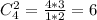
Так как выбор независим, то выбрать 4 точки можно то есть имеется 18 четырёхугольников.
ОТВЕТ: 18 четырёхугольников
1) Осевое сечение - прямоугольник ABCD высотой AB = 5 см, диагональю BD = 13 cм и длиной AD, равной диаметру цилиндра D =>
AD^2 = BD^2 - AB^2 = 13^2 - 5^2 = (13+5)(13-5) = 18*8 = 36*4 = 6^2 * 2^2 = 12^2 =>
AD = D = 12 см - диаметр основания =>
R = D/2 = 12/2 = 6 см - радиус