1) Вверх (старший коэф. больше нуля)
2) -3 и 0
x² + 3x = 0 ⇔ x(x + 3) = 0 ⇔ x1 = 0; x2 = -3
3) (-1,5; -2.25) смотри выделение полного квадрата ниже
4)
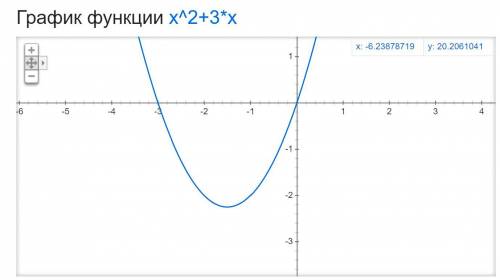
5) Возрастает при x > -1.5, убывает при x < -1,5 (см. график)
6) Наибольшего значения нет, наименьшее -2.25 (см. найденную вершину)
7) [-1.5; +∞) (см. график)
8) Ось симметрии x = -1.5 (см. график)
9) При x < -3 и x > 0 положительный, при -3 < x < 0 отрицательно (см. график)
Пошаговое объяснение:
Для начала надо выделить полный квадрат
x² + 3x = (x² + 2 * 1,5x + 1,5²) - 1,5² = (x + 1,5)² - 2,25
Советую выучить такие элементарные вещи, чтобы 2 не ставили...
Теорема Пифагора ⇒ с² = a² + b² ( гипотенуза в квадрате равна сумме квадратов катетов )
( 1 )
с² = a² + b²
CB² = AC² + AB²
CB² = 4² + 5²
CB² = 16 + 25
CB² = 41
CB = √41
Гипотенуза равна √41
( 2 )
с² = a² + b²
b² = c² - a²
BC² = AB² - AC²
BC² = 8² - 7²
BC² = 64 - 49
BC² = 15
BC = √15
Катет равен √15
( 3 )
ABM и MBC - два прямоугольных треугольника
AC = 16 см
AC : 2 = 16 : 2 = 8 см ( Длинна AM и MC )
Высота равнобедренного треугольника ABC является катетом прямоугольных треугольников ABM и MBC
Я буду рассматривать треугольник ABM , но так же можно найти катет и по треугольнику MBC
c² = a² + b²
a² = c² - b²
BM² = AB - AM
BM² = 17² - 8²
BM² = 289 - 64
BM² = 225
BM = √225
BM = 15
Высота равнобедренного треугольника ABC равна 15 см