1. 7,4
2. 16
3. 18
Пошаговое объяснение:
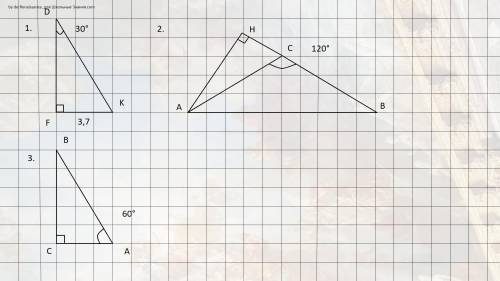
1. По свойству катета напротив угла в 30° (он равен половине гипотенузы) DK = 2FK = 3,7 * 2 = 7,4
2. ∠HCA = 180° - ∠ACB (смежные) = 180° - 120 ° = 60°. Рассмотрим прямоугольный треугольник HAB. По свойству углов при основании равнобедренного треугольника ∠ABC = (180° - ∠ACB) : 2 = 30°, откуда по свойству катета напротив угла в 30° AB = 2AH = 16
3. Напротив меньшего угла лежит меньшая сторона, и поэтому, ∠BCA = 90° - ∠BAC = 30° лежит напротив меньшего катета. По свойству катета напротив угла в 30° AC = 2BC => AC + BC = 3BC = 27 => BC = 9 => AC = 18
Пошаговое объяснение:
1. По теореме о катете, лежащем против угла в 30°, ОК=1/2*СК. ⇒
СК=2*ОК=2*7,6=15,2 см
2. Т. к. Δ равнобедренный, то углы при основании Δ =(180-120):2=60:2=30°. Высота, проведенная в тупоугольном треугольнике к боковой стороне, падает на ее продолжение. В получившемся при этом прямоугольном Δ, острый угол = 30°. По теореме, что и в 1-й задаче, основание данного Δ - это гипотенуза прямоугольного Δ = 2*5= 10 см
3. 90°-60°=30° - 2-й острый угол. Пусть меньший катет= х см, тогда (все по той же теореме) гипотенуза = 2х см. составим уравнение х+2х=36
3х=36. х=12. 2*12=24 см - длина гипотенузы.
Длина-? см.
Площадь-? см².
Периметр-? см.
1) 4×2=8 (см.)-длина.
2) S=8×4=16 (см²)-площадь.
3) P=(4+8)×2=24 (см)-периметр.
ответ: 16 см² площадь; 24 см периметр.