Тут мы должны учесть некоторое обстоятельство. В ящике шаров желтых 2, а мы должны вытащить четыре. Мы не можем этого сделать. Вероятность 0. Однако, я рассмотрю вероятность всех шаров, может в условии ошибка. Рассмотрим вероятность вытаскивания черного шара. Вероятность - число, равное отношению благоприятных событий к общему их количеству. Итак, вероятность для черных равна. 12\(12+7+2)=12\21. Вероятность вытаскивания желтого шара равна 2\21. Казалось, формула (((Вероятность вытаскивания черного шара)^(кол-во черных))*((Вероятность вытаскивания желтого шара)^(кол-во желтых))=ответ) работает. Но увы.
ответ: 0
Подробнее - на -
Пошаговое объяснение:
Пошаговое объяснение:
Вспоминаем свойства степеней, это алгебра 7-го класса. Фото внизу.
Задача 497.
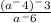
В этом примере необходимо раскрыть скобки. Св-во степени: при раскрытии скобок показатели степеней перемножаются.
Получаем:
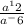
При делении показатели степеней вычитаются!
Получаем:
a^12 - (-6) = a^12+6 = a^18 (^ - степень).
Задача №498. (Попробуй решить самостоятельно).
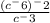
Тут опять же раскрытие скобок и деление. (Свойства при раскрытии скобок и делении выше!).
Получаем: c^12-(-3) = c^15 (^ - степень!)
Задача 499.
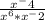
Тут для начала надо разобраться с знаменателем дроби: при умножении степени складываются.
Получаем:
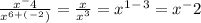
Задача 500.
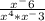
Производим манипуляции со степенями в знаменателе(степени при умножении складываются) и получаем:
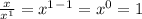
И вот тут еще одно свойство степеней: число, которое возводят в нулевую степень, будет всегда равно единице.
Задача 501.
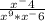
И опять мы делаем свои дела в знаменателе, получаем дробь:
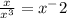
Задача 502.
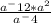
Делаем свои дела уже в числителе. Получим дробь:
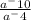 = a^-6
= a^-6
Не забудь, что при делении степени вычитаются!

2,46
2,64
35,6
6,05