ответ: Постарался доказать как можно более строго.
Пошаговое объяснение:
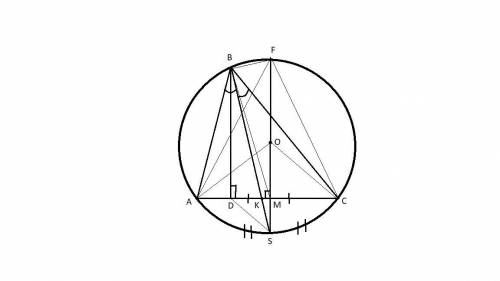
Рассмотрим неравнобедренный Δ ABC
Опишем около Δ ABC окружность .
Проведем к стороне AC отрезок OM и продлим его до диаметра окружности FS.
Δ AOC - равнобедренный, поскольку OA = OС как радиусы окружности. Таким образом, его медиана OM (M делит AC пополам) является и его высотой, но тогда и медиана FM треугольника AFC является его высотой, а значит он так же равнобедренный. Но тогда, эта высота является и биссектрисой, то есть ∠AFS =∠SFC, причем эти углы вписаны в окружность, а значит опираются на равные дуги. Иначе говоря, дуга AS равна дуге SC, но тогда и вписанные углы ∠ABS = ∠SBC .
Таким образом, BS биссектриса ∠B треугольника ABC , пусть она пересекает сторону AC в точке K.
BD ║ FS как два перпендикуляра к одной прямой AC, то есть SDBF - трапеция, а ЛЮБАЯ трапеция является выпуклым четырехугольником, причем BS ее диагональ. Теперь придется сослаться на одну аксиому, а именно, что все точки диагонали выпуклого четырехугольника лежат внутри четырехугольника, но тогда и точка K лежит внутри трапеции (K∈SDBF).
Геометрическое место точек, принадлежащих и трапеции и отрезку AC - это отрезок DM.
Таким образом, раз точка K∈AC и K∈ SDBF , то K∈DM
Что и требовалось доказать.
Пошаговое объяснение:
sin( п/3-a)=sin pi/3*cos a - cos pi/3 *sin a= корень из 3/2 * cos a - 1/2* sin a = 1/2*( cos a * корень из 3 - sin a) =1/3
cos a * корень из 3 - sin a =2/3
sina = корень из (1- cos ^2 a)
Пусть cos a =x
x * корень из 3 - корень из (1 - x^2)= 2/3
Возведем в квадрат обе части уравнения
(x * корень из 3 - корень из (1 - x^2))^2= 4/9
(x * корень из 3)^2 - 2x * корень из 3 *корень из (1 - x^2)) +(1 - x^2)=4/9
3x^2-2x*корень из(3(1 - x^2))+1-x^2=4/9
2x^2-2x*корень из(3 - 3x^2)+1-4/9=0
x^2-x*корень из(3 - 3x^2)+5/9=0
D=(корень из(3 - 3x^2)^2-4*1*5/9
1,5*(х+12) = 24
1,5х+18 = 24
1,5х=24-18
1,5х=6
х=6:1,5
х=4
ответ 4км/ч