Нехай ABCD - заданий прямокутник, O - точка перетину діагоналей, AB=4, кут AOB = 60 градусів, АС - шукана діагональ
Розв'язання
Оскільки АBCD - прямокутник, його діагоналі рівні й точкою перетину діляться навпіл, тому АО=ВО. Отже, трикутник АОВ - рівнобедренний
За умовою кут АОВ дорівнює 60 градусів. Тоді кути при основі трикутника АОВ рівні і дорівнюють (180-60)/2=60 градусів. Оскільки у трикутника АОВ всі кути рівні, він - рівносторонній
Тоді АО=ВО=АВ=4(см)
Оскільки АО=ОС, АС = 4+4=8(см)
Відповідь: 8 см
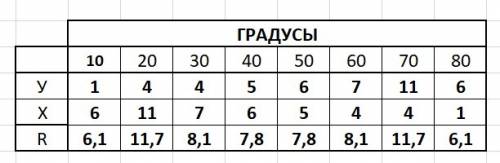
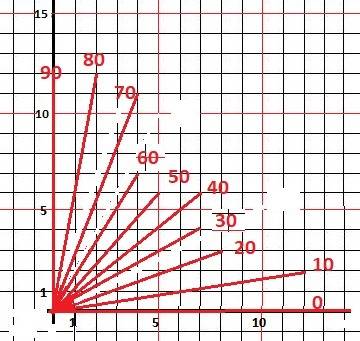
1) Берём транспортир и делаем рисунок до пересечения с узлом сетки - в приложении.
2) Заполняем таблицу с результатами измерений. Узел обозначаем точкой на рисунке и двумя координатами в таблице. Таблица в приложении. А на рисунке они не обозначены, чтобы их было видно.
3) Определить путь - измерить расстояние линейкой между этими точками и началом координат. Можно и вычислить по теореме Пифагора гипотенузу: c = √(x²+y²).
4) Сравнить результаты - отношения Х и У - обратные -
1/6 и 6/1, 4/11 и 11/4, а длины отрезков - равные.
5) Построить силой Разума угол примерно 30° - запросто - семь направо четыре вверх.
Дополнительно.
45° = 1/1.