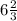
Пошаговое объяснение:
Коли функция 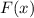 - первообразная для функции
- первообразная для функции 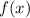 , то функция производной от функции
, то функция производной от функции 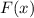 .
.
Имея производную мы можем найти локальные максимумы и минимумы функции. Для этого найдем точки, в которых производная равняется 0.

 - уравнение не имеет действительных корней.
- уравнение не имеет действительных корней.
Значит функция монотонно убывающая или монотонно возрастающая.
Ветви параболы направлены вверх, значит функция монотонно возрастающая.
Также это означает, что максимальное и минимальные значения функция принимает на концах заданного отрезка - [0; 2].
F(0) - минимальное значение на отрезке. Значит F(2) - максимальное значение на отрезке [0; 2].
Вычислим это значение.
Для начала, найдем функцию F(x). Для этого проинтегрируем её производную:
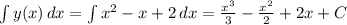
Это выражение задаёт целое семейство функций, различающихся на C = const.
Теперь найдем среди этого семейства нужную нам функцию. По условию у нас дано частное значение функции 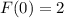
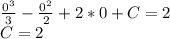
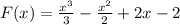
Вычислим 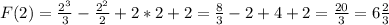
написал в обьяснении Пошаговое объяснение:
а) Каждый пират должен получить (40 + 40 * 5) : 16 = 15 дукатов. Выдадим 13 пиратам по 3 монеты достоинством 5 дукатов, одному — 5 дукатов и 10 монет достоинством 1 дукат, двоим — по 15 монет достоинством 1 дукат.
б) Каждый пират должен получить 240 : 30 = 8 дукатов, поэтому нужно будет выдать каждому не менее трёх монет достоинством 1 дукат, значит всего монет достоинством 1 дукат нужно не менее 90 штук, а в сундуке их только 40. Следовательно, без сдачи и размена поделить все монеты поровну не получится.
в) Если пиратов 12 или больше, то распределим монеты так: 10 пиратов получают по 4 дуката, один — всё остальное, остальные — ничего. Тогда распределить все монеты нельзя будет по тем же причинам, что и в пункте б).
Если же их не больше 11, то всем, кроме одного, будем выдавать их доли монетами достоинством 5 дукатов, пока они не кончатся.
Если монеты достоинством 5 дукатов закончились, то останется 40 монет достоинством 1 дукат, а их можно разделить на любые целые числа. Если же монеты достоинством в 5 дукатов не кончились, то все доли, кроме одной, можно выдать до конца монетами по 1 дукату (поскольку их получат не более 10 человек, значит, израсходуется не более 40 монет достоинством 1 дукат), а последний заберёт все оставшиеся монеты.
ответ: они встретятся через 4 часа.